.
See the link
https://www.quora.com/If-u-v-w-x-y-15-then-what-is-the-maximum-value-of-uvx-uvy-uwx-uwy
the answer by Daniel Claydon. Below I copy-pasted from there.
-----------------
Notice that
uvx + uvy + uwx + uwy = u(x+y)(v+w).
If u, v, w, x, y are allowed to be negative, there is no largest value, since, for example,
one could let u, x, y be arbitrarily “large” negative numbers (so u(x+y) is positive),
then v+w is a large positive number and the whole product can be as large as you like.
If they are restricted to positive real numbers, then from AM-GM, we have
>= 
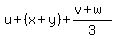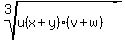Using the imposed condition to the sum, the left side is just 5, so we have found
} <= 
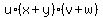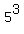= 125.
The maximum value is 125, and occurs if, and only if, u = x+y = v+w = 5.
