.
Find: limit 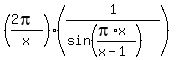 when x→ + ∞
when x→ + ∞
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 =
= 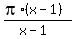 +
+  =
=  +
+  . (1)
Therefore, sin((pi*x)/(x-1)) = sin(pi + pi/(x-1)) =
. (1)
Therefore, sin((pi*x)/(x-1)) = sin(pi + pi/(x-1)) = 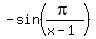 . (2)
When x→ + ∞, (x-1) is large value;
. (2)
When x→ + ∞, (x-1) is large value;  is a small value;
therefore,
is a small value;
therefore,  is a small value equivalent to
is a small value equivalent to  .
It implies that
.
It implies that  is a negative value equivalent to
is a negative value equivalent to  .
Then
.
Then 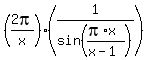 is equivalent to
is equivalent to 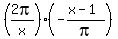 .
As x→ + ∞, the quantity
.
As x→ + ∞, the quantity 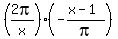 tends to -2.
Thus limit
tends to -2.
Thus limit 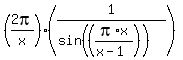 is -2 when (x→ + ∞).
is -2 when (x→ + ∞).
Solved.