Question 1199691: Solve 2x-1 < (x+7)/(x+1) algebraically
Found 3 solutions by josgarithmetic, greenestamps, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The partial solution method shown by the other tutor will lead to the wrong answer, because it uses an invalid step.
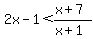
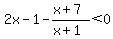
You can't multiply everything by (x+1) here, because for some values of x (x+1) is negative, and for one particular value of (x+1) is zero. We need to keep the denominator in our solution.
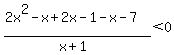
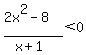
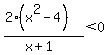
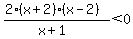
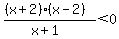
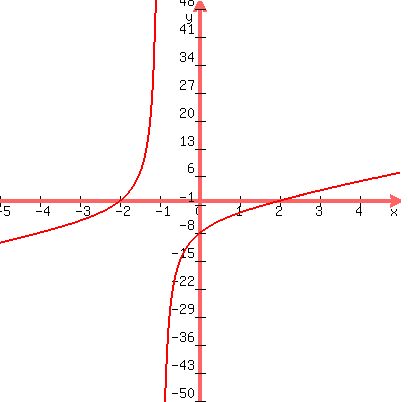
The value of the expression on the left changes sign only when one of the factors in the numerator or denominator changes sign; that happens only at x = -2, x = -1, and x=2.
Looking at the intervals determined by those three values of x, you will see that the expression is negative on (-infinity,-2) and (-1,2); it is positive or zero on [-2,-1) and on [(2,infinity).
ANSWER: (-infinity,-2) U (-1,2)
Here is a graph showing that 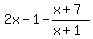 is negative on exactly those intervals.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Solve 2x-1 < (x+7)/(x+1) algebraically
Contrary to what the other person states, you CAN multiply by the LCD, x + 1
Since denominator is x + 1, it follows that: 
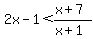(2x - 1)(x + 1) < x + 7 ----- Multiplying by LCD, x + 1
(x - 2)(x + 2) < 0
x - 2 < 0 OR x + 2 < 0
x < 2 OR x < - 2
Since 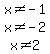 , - 2, - 1, and 2 will be the CRITICAL points.
With the 3 CRITICAL POINTS above, we get the 4 TEST INTERVALS:
x < - 2___x = - 3 - 2 < x < - 1___x = - 1.5 -1 < x < 2__x = 0 x > 2___x = 3
   
Solution sets: x < - 2, and - 1 < x < 2 since these are the ONLY TRUE STATEMENTS.
In INTERVAL NOTATION, we get: ( ) ( )
|
|
|
