SOLUTION: Determine the distance from the curve x^2 + y^2 - 16y + 16x + 64 = 0 to point (6,4). A. 6.56 B. 5.24 C. 7.52 D. 4.16

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Determine the distance from the curve x^2 + y^2 - 16y + 16x + 64 = 0 to point (6,4). A. 6.56 B. 5.24 C. 7.52 D. 4.16      Log On


   

Question 1199589: Determine the distance from the curve x^2 + y^2 - 16y + 16x + 64 = 0 to point (6,4).
A. 6.56
B. 5.24
C. 7.52
D. 4.16
Answer by ikleyn(52914) About Me  (Show Source):
You can put this solution on YOUR website!
.

Apply completing the squares method and reduce the given equation to equation

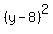    %28x%2B8%29%5E2 + %28y-8%29%5E2 = 64.


It is equation of the circle of the radius 8 units centered at point (-8,8) .


The point (6,4) is at the distance

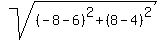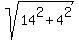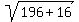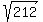    sqrt%28%28-8-6%29%5E2+%2B+%288-4%29%5E2%29 = sqrt%2814%5E2%2B4%5E2%29 = sqrt%28196%2B16%29 = sqrt%28212%29 = 14.56   (rounded)

from the center of that circle.


Hence, the distance from the given point to the circle is  14.56 - 8 = 6.56 units, approximately.

Solved.