|
Question 1199585: The towers of a 60 meter parabolic suspension bridge are 12 m high and the lowest point of the cable is 3 m above the roadway. Find the vertical distance from the roadway to the cable at 15 m from the center.
A. 3 m
B. 6 m
C. 5 m
D. 8 m
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The towers of a 60 meter parabolic suspension bridge are 12 m high and the lowest point
of the cable is 3 m above the roadway. Find the vertical distance from the roadway
to the cable at 15 m from the center.
A. 3 m
B. 6 m
C. 5 m
D. 8 m
~~~~~~~~~~~~~~~~~~~~
If we place the origin of the coordinate system at the bridge level midpoint between the two towers,
we have the vertex of the parabola at the point (0,3).
So, we write an equation of the parabola in vertex form
y = ax^2 + 3.
Coefficient "a" is unknown. It is the only unknown in this problem now.
To find it, we use the condition at the endpoint: y= 12 at x= 60/2 = 30. It gives
12 = a*30^2 + 3
12 - 3 = a*900
9 = 900a
a = 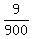 = =  .
Thus the parabola is y = .
Thus the parabola is y = 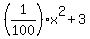 .
Having this equation ready, we substitute x =15 meters into the equation
and find the height of the cable at the point x= 15, which is 15 meters from the midpoint of the bridge
y = .
Having this equation ready, we substitute x =15 meters into the equation
and find the height of the cable at the point x= 15, which is 15 meters from the midpoint of the bridge
y = 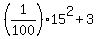 = 2.25 + 3 = 5.25 m (rounded). ANSWER = 2.25 + 3 = 5.25 m (rounded). ANSWER
Solved.
----------------
The problem can be solved mentally, without using equations, but using common sense, instead.
Half-length of the bridge between the towers is 60/2 = 30 m.
The point of the interest is at 15 m, half of the bridge's half-length, from the midpoint.
So, the height of the cable above the bridge is 3 m PLUS 1/4 of the cable levels difference between
the midpoint position and the tower position
height = 3 + 1/4*(12-3) = 3 + 1/4*9 = 3 + 2.25 = 5.25 m,
exactly the same as we obtained it above.
This value 5.25 m is close to the value 5 of the answer option C.
|
|
|
| |