Let's see what you did:
x-[x-(y-z)]-z
-1(y-z) I took the - as -1 and multiplied it by (y-z)
That was right. And you got -1y+1z and then you dropped the 1's
and gotten -y+z. That was correct.
x(-y+z) expanded and multiplied by x
No. That's wrong. The x is separated from the (y-z) by a minus. It's not
x(-y+z). It's x-(-y+z). There is a - between the x and the (-y+z). So
there is another -1 understood before the remaining parentheses. There is
no multiplication when something separated by a plus or minus sign. What
you did wrong was to ignore the minus sign between the x and the
remaining parentheses. You should have thought of it like you did
at first with the -1, and had x-1(y+z) then x-1y-1z and dropped the 1's.
--------------------------------------------
This is how I would do it:
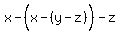Remove the innermost parentheses -(y-z) first. It's preceded by a minus,
so I change the sign of y inside to -y and change the sign of -z to +z.
So instead of -(y-z) write -y+z:
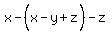Now remove the remaining parentheses. It's also preceded by a minus,
so change the sign of x inside to -x, change the sign of -y inside to +y,
and change the sign of +z to -z.
So instead of -(x-y+z) write -x+y-z instead:
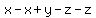Now x-x just becomes 0 so we just eliminate x-x. Then we replace -z-z
by -2z. That's because we think of -z-z as if it were -1z-1z, and when you
add two negatives you get another negative:
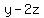Edwin
