SOLUTION: A rectangle is 5 cm longer than its width. If its width is x cm and its area is 14 cm2. a)Form an equation in x. b)Solve the equation to find the value of x. (c) State the dimens

The width is x cm.

The length is (x+5) cm.


The area of a rectangle is the product of the length by the width.


Therefore, the area equation for this problem is 

    x*(x+5) = 14.     (1)


It can be transformed to the standard form quadratic equation

    x^2 + 5x = 14,

    x^2 + 5x - 14 = 0.     (2)


This quadratic equation can be solved in two ways: using the quadratic formula or by factoring.


The solution by factoring is extremely short and easy:  we factor left side as the product 

    x^2 + 5x - 14 = (x+7)*(x-2).


Therefore, equation (2) takes the form

    (x+7)*(x-2) = 0.


It has two roots,  x= -7  and  x= 2.


In this problem, x is the width of a rectangle, so we are seeking for the positive value.


Therefore, we accept the positive value x= 2 and reject the negative value x= -7.


Thus the problem is just solved, and the answer is


    the width of the rectangle is  2 cm; its length is  2+5 = 7 cm.


CHECK.  2*7 = 14 cm^2, which coincides with the given area and confirms the answer.


In this way, the solution is complete.



If you want, you may use the quadratic formula, too.  It gives the roots

     =  =  = .


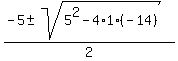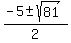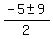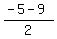Thus   =  = 2;   =  = -7,  and we get the same roots.


Due to the same reason, we accept the positive root and reject the negative one.