Question 1199445: A circle passes through the points (6,3), (6,-3) and (2,5).Find the centre,radius, and equation of the circle
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A circle passes through the points A(6,3), B(6,-3) and C(2,5). Find the centre, radius, and equation of the circle
------------
Find the perpendicular bisectors of AB and AC.
For AB, it's the x-axis.
---
For AC:
Find the midpoint:
x: (6+2)/2 = 4
y: (3+5)/2 = 4
(4,4) is the midpoint
---
The slope of AC is (5-3)/(2-6) = -1/2
The slope of lines perpendicular to AC = 2
-----
Thru (4,4) with m = 2 ---> y-4 = 2(x-4)
y = 2x-4 is the equation of the perpendicular bisector to AC
----
The intersection of y = 2x-4 and the x-axis is the center of the circle.
At the x-axis, y = 0
0 = 2x-4 ---> x = 2
The center is (2,0)
-----
The radius is the distance between the center and any of the 3 given points.
r^2 = diffy^2 + diffx^2
r^2 = (3-0)^2 + (6-2)^2 = 25
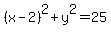
|
|
|