Question 1199347: If tan(x/2)=sinx and cosx≠0, then the value of tanx is…
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If tan(x/2)=sin(x) and cos(x)≠0, then the value of tan(x) is . . .
~~~~~~~~~~~~~~~~~~
Our starting equation is
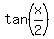 = =  . (1)
Since . (1)
Since 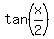 is not defined when is not defined when 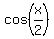 = 0, the domain of this equation is
the set of all real numbers except = 0, the domain of this equation is
the set of all real numbers except  = = 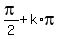 , or x = , or x = 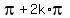 = = 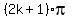 .
One obvious solution to equation (1) is x = .
One obvious solution to equation (1) is x =  , when both sides of equation (1) are zeroes. (2)
In what follows, we assume that x is neither , when both sides of equation (1) are zeroes. (2)
In what follows, we assume that x is neither  nor nor 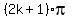 . (3)
In particular, it implies that . (3)
In particular, it implies that  =/= 0. (4)
Now we transform equation (1) step by step =/= 0. (4)
Now we transform equation (1) step by step
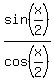 = = 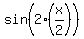
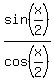 = =  Due to (4), we can divide both sides by
Due to (4), we can divide both sides by  , since this factor is not zero. , since this factor is not zero.
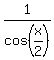 = = 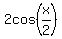
 = = 
 = = 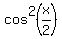
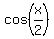 = = 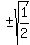 = = 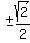
 = =  <<<---=== notice here the difference with the Edwin's solution
(here Edwin lost some/(half of the) solutions) <<<---=== notice here the difference with the Edwin's solution
(here Edwin lost some/(half of the) solutions)
 = = 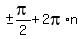 = = 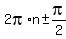 = = 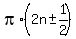 , where n is any integer.
But for all these values of x, cos(x) = 0, so we should exclude this set of values
from our consideration due to condition cos(x) =/= 0, imposed in the problem.
Finally, the only set of solutions is x = , where n is any integer.
But for all these values of x, cos(x) = 0, so we should exclude this set of values
from our consideration due to condition cos(x) =/= 0, imposed in the problem.
Finally, the only set of solutions is x =  , found in (2).
ANSWER. The solution to equation (1) with the imposed condition cos(x) =/= 0
is the set x = , found in (2).
ANSWER. The solution to equation (1) with the imposed condition cos(x) =/= 0
is the set x =  , and tan(x) = 0 for all these values of x. , and tan(x) = 0 for all these values of x.
Solved.
|
|
|