Question 1199346: If a < b, show that a < (a + b)/2 < b.
Note: The number (a + b)/2 is called the arithmetic mean of a and b.
Can someone get me started by providing the first-two steps?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
If a < b, show that a < (a + b)/2 < b.
Note: The number (a + b)/2 is called the arithmetic mean of a and b.
Can someone get me started by providing the first-two steps?
~~~~~~~~~~~~~~~~~
Write this equality/(identity), which is true for any/each value of "a"
a =  + . (1)
In this equality, replace the second addend by the greater value  .
Doing this way, from equality (1) you will get then INEQUALITY
a < + . (2)
It is the same as
a < 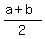 . (3)
Thus, first part of the statement is proved.
+---------------------------------------------------+
| From this point, I continue for the second part. |
+---------------------------------------------------+
Write this equality/(identity), which is true for any/each value of "b"
+ = b. (4)
In this equality, replace first addend by the lesser value .
You will get then INEQUALITY
+ < b. (5)
It is the same as
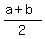< b. (6)
Combining (3) and (6) together in one compound inequality, we get
a < 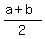< b,
QED.
Solved and explained.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
a < (a+b)/2 < b
breaks into
a < (a+b)/2 and (a+b)/2 < b
Let's do a bit of algebraic operations on the first inequality we've broken down
a < (a+b)/2
a < 0.5(a+b)
a < 0.5a+0.5b
a-0.5a < 0.5b
0.5a < 0.5b
a < b
Reverse those steps:
a < b
0.5a < 0.5b
0.5a+0.5a < 0.5b+0.5a
a < 0.5a+0.5b
a < 0.5(a+b)
a < (a+b)/2
We can also say the following:
a < b
0.5a < 0.5b
0.5a+0.5b < 0.5b+0.5b
0.5(a+b) < b
(a+b)/2 < b
With a < b as our starting point for the last two subsections, we've found that
a < (a+b)/2 and (a+b)/2 < b
which combines into
a < (a+b)/2 < b
Therefore, the claim has been proven.
----------------------------------------------------
Another approach:
Let
c = a+b
Add 'a' to both sides of the original inequality.
a < b
a+a < b+a
2a < a+b
2a < c
Now add 'b' to both sides
a < b
a+b < b+b
c < 2b
Since 2a < c and c < 2b, we know that 2a < c < 2b.
Then as a last set of steps:
2a < c < 2b
2a < a+b < 2b
2a/2 < (a+b)/2 < 2b/2
a < (a+b)/2 < b
|
|
|
