SOLUTION: Hi Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed. At the same time a bus leaves x for y travelling at a constant speed. The two pa

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Hi Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed. At the same time a bus leaves x for y travelling at a constant speed. The two pa      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1199336: Hi
Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed. At the same time a bus leaves x for y travelling at a constant speed. The two pass each other at 1.20pm . The average speed of the van is 60km per hour faster than the bus.
Find the vans average speed. How far is the bus from x when it passes the van.
Thanks
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
Both the van and the bus left from x at the same time. They do not pass each other.


Did you REALLY mean this way?
-----------------------------------------------------------------------------
Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed. At the same time a bus leaves y for x travelling at a constant speed. The two pass each other at 1.20pm . The average speed of the van is 60km per hour faster than the bus.
Find the vans average speed. How far is the bus from x when it passes the van.
-----------------------------------------------------------------------------


If one is going toward the other starting from the two separate towns, and ONLY IF so, then
van travels from x to y
bus travels from y to x

         SPEEDS           TIMES             DISTANCE

VAN       v               2%261%2F3           %287%2F3%29v

BUS       v-60            2%261%2F3           %287%2F3%29%28v-60%29

TOTAL                                  560

%287%2F3%29%28v%2B%28v-60%29%29=560
%281%2F3%29%282v-60%29=80
2v-60=240
v-30=120
highlight%28150%29kilometers%2Fhour-------speed of the van
highlight%2890%29-----------------speed of the bus


---

Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed.
At the same time a bus leaves x for y travelling at a constant speed. The two pass each other at 1.20pm .
The average speed of the van is 60km per hour faster than the bus.
Find the vans average speed. How far is the bus from x when it passes the van.
~~~~~~~~~~~~~~~~~~~


The problem's formulation is absurdist and incorrect.



Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!

Hi
Town x and town y are 560km apart. At 11am a van leaves x for y travelling at a constant speed. At the same time a bus leaves x for y travelling at a constant speed. The two pass each other at 1.20pm . The average speed of the van is 60km per hour faster than the bus.
Find the vans average speed. How far is the bus from x when it passes the van.
Thanks
They can't PASS EACH OTHER if they leave the same location and are heading in the same direction. One must've left x heading to y, 
and the other, y heading to x.
That way, van's speed would be 150 km/h, NOT 240 km/h as the other person claims.

With the van heading to y, at 150 km/h, 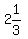2%261%2F3 hours after leaving x, it would've covered 
This is where they pass each other, which is also the distance that the bus is, from x.
OR
Calculate the distance the bus traveled from y to the "passing" point, and then subtract that from 560 km. The result should be the same!