Question 1199329: The increasing sequence T = 2 3 5 6 7 8 10 11 consists of all positive integers which are not perfect squares. What is the 2012th term of T?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
2012 is a bit less than 45^2 = 2025, so there are 44 perfect squares less than 2012.
2012-44 = 1968, so the number 2012 is the 1968-th term in the sequence.
To find the 2012-th term, we need to add 44 more terms, which means adding 44 to 2012, to get 2056. But one of the numbers between 2012 and 2056 is another perfect square, so we need to go one number farther, to 2057.
ANSWER: the 2012-th term in the sequence is 2057.
There are of course different paths of logical reasoning to arrive at the answer....
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The increasing sequence T = 2 3 5 6 7 8 10 11 consists of all positive integers
 that are not perfect squares. What is the 2012th term of T? that are not perfect squares. What is the 2012th term of T?
~~~~~~~~~~~~~~~~~~~~~~~
This problem has an underwater stone like a trap.
We should be careful in order for not to fall into the trap.
In the course of my solution, I will show you where the trap is
and what to do to avoid falling into the trap.
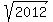 = 44.86 (rounded).
So, the original sequence was the sequence of all natural numbers, starting from 1
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, . . .
from which 44 terms (perfect squares) were excluded.
Hence, one can think that the 2012-th term of the given sequence is
the (2012 + 44)-th term of the sequence of all natural numbers, starting from 1,
which is the number (2012 + 44) =2056.
+-----------------------------------------------------------------------+
| Here is the trap. To avoid falling into the trap, we should check |
| if there is a perfect unaccounted square between = 44.86 (rounded).
So, the original sequence was the sequence of all natural numbers, starting from 1
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, . . .
from which 44 terms (perfect squares) were excluded.
Hence, one can think that the 2012-th term of the given sequence is
the (2012 + 44)-th term of the sequence of all natural numbers, starting from 1,
which is the number (2012 + 44) =2056.
+-----------------------------------------------------------------------+
| Here is the trap. To avoid falling into the trap, we should check |
| if there is a perfect unaccounted square between 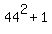 and 2056. |
+-----------------------------------------------------------------------+
So, we check the next perfect square and 2056. |
+-----------------------------------------------------------------------+
So, we check the next perfect square 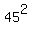 = 2025, and we see that
such a perfect square does really exist.
Therefore, we make a correction to the previous estimate and conclude that
the 2012-th term is the number 2057, one unit greater than the previous estimate of 2056.
ANSWER. The 2012-th term of the described sequence is 2057. = 2025, and we see that
such a perfect square does really exist.
Therefore, we make a correction to the previous estimate and conclude that
the 2012-th term is the number 2057, one unit greater than the previous estimate of 2056.
ANSWER. The 2012-th term of the described sequence is 2057.
Solved.
|
|
|