Question 1199312: let O(0,0), A(6,0), B(6,6), c(0,6) be the vertices of a square OABC, and Let M be the midpoint of OB. Find the probability that a point chosen at random from the square is
a) father from O than from M
b) more than twice as far from O as from M
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
let O(0,0), A(6,0), B(6,6), c(0,6) be the vertices of a square OABC, and Let M be the midpoint of OB.
Here is a sketch:
a) Find the probability that a point chosen at random from the square is farther from O than from M.
To do this, determine where the points are that are the same distance from O as they are from M. This is simple; they lie on the perpendicular bisector of segment OM.
Note that this result can be obtained algebraically by solving the equation that says the distance from P(x,y) to O(0,0) is the same as the distance from P(x,y) to M(3,3):
(I won't do that in my response; however, it would be a good exercise for the student to solve this equation and find that indeed the set of points equidistant from O and M are the points on the line x+y=3.)
It should be easy to see from the sketch that the points in the square that are farther from O than from M constitute exactly 7/8 of the square. So
ANSWER to part a): 7/8
b) Find the probability that a point chosen at random from the square is more than twice as far from O as from M.
To solve this part, we could find the points that are EXACTLY twice as far from O as from M by solving the equation
(Again I won't do that here in my response; and again it would be a good exercise for the student to do so. You should find that the circle is centered at (4,4) with radius 2*sqrt(2).)
The set of points exactly twice as far from O as from M is a circle. Two of those points are (2,2) and (6,6); and by symmetry the segment joining those two points is a diameter of the circle.
Here is a sketch:
To answer this part of the problem, we need to find what fraction of the square is inside the circle.
The region of the square inside the circle consists of a semicircle plus an isosceles right triangle determined by the segment from (6,2) to (2,6). The radius of the circle is 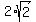 and the lengths of the legs of the triangle are 4, so the area of the semicircle is  and the area of the triangle is  .
The area of the whole square is 36, so the probability that a random point in the square is more than twice as far from O as it is from M is
ANSWER to part b): 
|
|
|
