Question 1199306: Question
(a) Determine whether the differential equation
ydx - xdy =0 is exact:
(b) If not, convert it into an exact differential equation_ (c) Solve this differential equation.
Found 3 solutions by Edwin McCravy, ikleyn, mccravyedwin:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Below is my note to the solution by Edwin.
I fully agree on how Edwin deduced equation
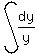  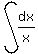 (*)
But what follows, should be corrected, because (*)
But what follows, should be corrected, because
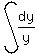 is not ln(y): it is ln(|y|); is not ln(y): it is ln(|y|); 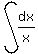 is not ln(x): it is ln(|x|)
with y =/= 0; with x =/= 0.
Therefore, from (*) we have
ln(|y|) = ln(|x|) + ln(C), x =/= 0; y =/= 0
y = Cx, with x =/= 0,; y =/= 0; C may have any sign, positive or negative, except C = 0. is not ln(x): it is ln(|x|)
with y =/= 0; with x =/= 0.
Therefore, from (*) we have
ln(|y|) = ln(|x|) + ln(C), x =/= 0; y =/= 0
y = Cx, with x =/= 0,; y =/= 0; C may have any sign, positive or negative, except C = 0.
////////////////
It is with regret I see that Edwin (@mccravyedwin) ascribes to me what I did not say and did not write.
Edwin, it is a prohibited way to make a discussion.
I said what I said, and what I said was right.
Happy New Year !
Answer by mccravyedwin(406)   (Show Source): (Show Source):
|
|
|