Question 1199271: All of the arrangements of the letters in the word ALGEBRA are written on a list, one of these arrangments selected at random. What is the probability that the arrangement contains a double-A
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52800)   (Show Source):
You can put this solution on YOUR website! .
All of the arrangements of the letters in the word ALGEBRA are written on a list,
one of these arrangments selected at random.
What is the probability that the arrangement contains a double-A
~~~~~~~~~~~~~~~~~~
There are 7 letters in the word "ALGEBRA", in all; of them, only letter "A" repeats twice.
The table below shows the number of distinguishable arrangements with 1, 2, 3, 4, 5, 6 and 7 letters.
In the 2nd and 3rd columns, the formula is used nPk = n*(n-1)*...*(n-k+1).
In the second column, n=5. In the third column, n=6.
# of # of arrangements # of arrangements # of arrangements
letters without "A" with one "A" with two "A"s
k used 5Pk 6Pk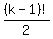 
--------------------------------------------------------------------
1 5 6 -
2 20 30 1
3 60 120 3
4 120 360 12
5 120 720 60
6 - 720 360
7 - - 2520
Total 325 1956 2956
The probability that the arrangement contains a double-A = 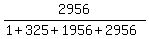 =  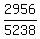= 0.5643 (rounded).
The "1", added in the denominator, is for empty arrangement.
ANSWER. The probability that the arrangement contains a double-A is 0.5643 (rounded).
Solved.
--------------
The major lesson to learn from this solution is how to organize your thoughts and your calculations.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
My interpretation of "all of the arrangements of the letters in the word ALGEBRA" is that all 7 letters are used in each arrangement.
Here are two ways to find the probability that the two A's are next to each other when all 7 letters are used.
(1) Counting numbers of permutations....
The number of ways of arranging the 7 letters is 7!
For the number of ways of having the two A's together, treat those two letters as a unit. We are now arranging 6 items; there are 6! arrangements, and the two A's can be in either of two orders. So the number of arrangements of the 7 letters with the two A's together is 2*6!.
The probability of having the two A's together is then
(2) Considering the different places in the string where the two A's are together....
If the first A is in either the first or last position (probability 2/7), then there is only one of the other 6 positions where the second A can be (probability 1/6). The probability for this case is (2/7)(1/6) = 2/42.
If the first A is in any of the other 5 positions (probability 5/7), then the second A can be in either of two of the other 6 positions (either side of the first A -- probability 2/6). The probability for this case is (5/7)(2/6) = 10/42.
The overall probability is then 2/42 + 10/42 = 12/42 = 2/7.
ANSWER: 2/7
|
|
|
