Question 1199213: A candy manufacturer makes two types of special candy, say A and B. Candy A consists of equal
part of dark chocolate and caramel and Candy B consists of two parts of dark chocolate and one
part of walnut. The company has in stock 430 kilograms of caramel, 360 kilograms of dark
chocolate, and 210 kilograms of walnuts. The company sells Candy A for P285 and Candy B for
P260 per kilograms. How much of each candy should the manufacturer produce to maximize profit?
Found 2 solutions by Shin123, ikleyn:
Answer by Shin123(626)   (Show Source):
You can put this solution on YOUR website! Let  be the amount (in kilograms) of Candy A that is produced, and let  be the amount of Candy B that is produced. The profit that the manufacturer makes is 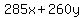 . However, the constraints are that  ,  , and  .
We can see that it is optimal to have  , since moving it off of that line would only decrease the profit. Multiplying both sides of that by  , we get  . Adding 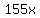 to both sides, we get  . We can see that we got out profit into a form that doesn't involve at all, so we should just maximize . The highest value of that satisfies all of the constriants is  . Therefore, the candy manufacturer should produce  kilograms of Candy A, and  kilograms of Candy B.
Answer by ikleyn(52790)  (Show Source):
You can put this solution on YOUR website! .
A candy manufacturer makes two types of special candy, say A and B. Candy A consists of equal
part of dark chocolate and caramel and Candy B consists of two parts of dark chocolate and one
part of walnut. The company has in stock 430 kilograms of caramel, 360 kilograms of dark
chocolate, and 210 kilograms of walnuts. The company sells Candy A for P285 and Candy B for
P260 per kilograms. How much of each candy should the manufacturer produce to maximize profit?
~~~~~~~~~~~~~~~~~~~
Let x = kilograms of Candy A,
y = kilograms of Candy B.
Then A uses  kg of dark chocolate and kg of caramel;
B uses  kg of dark chocolate and  kg of walnut.
The restrictions from the problem are
<= 430 (1) (caramel)
+ <= 360 (2) (dark chocolate)
<= 210 (3) (walnut)
x >= 0, y >= 0 (4) (non-negativity)
The profit function is P(x,y) = 285x + 260y.
By riding from the denominators in (1), (2) and (3), we get the standard form of the linear minimax problem
Maximize p = 285x + 260y subject to
x <= 860
3x + 4y <= 2160
y <= 630
x >= 0
y >= 0
Now go to web-site https://www.zweigmedia.com/RealWorld/simplex.html
and use free of charge online solver specially intended for such Linear Programming problems.
Copy-paste this standard input above to the input window port of the solver and click the button "Solve".
You will get the answer x = 720, y = 0, p = 205200.
So, the optimal strategy is to produce and to cell 720 kg of candy A only
and do not produce candy B, at all.
It gives the maximum profit of Php 205200.
Solved.
-----------------
In the post by @shin123, the reasoning for deriving the constraints is incorrect, and his constraints are incorrect, too,
although the final answer is correct and coincides with my answer.
In this problem, the major interest is to create a correct setup, so I concentrated on it.
Making a correct setup was my primary goal.
The technique of solving plays a subordinate role in this problem,
so and therefore, I used the automatic online solver (software) to save my time.
The problem also can be solved mentally, based on common sense.
Indeed, it is clear that the constraint for walnut does not work, actually: it is not a working constraint:
there are enough walnut for any purposes.
Next, looking on the input numbers, it is clear, that it is more profitable to make candy A only and to use full amount
of the chocolate for this purpose, since candy A bring more profit and resources allow to use the chocolate in full.
The only working constrain in this problem is the dark chocolate constrain (2).
It controls (governs) the entire problem.
|
|
|
