.
Simplify: 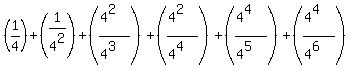 + ... +
+ ... + 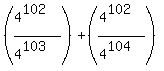
~~~~~~~~~~~~~~~~~~~~~~~~~
I see two sequences alternate.
After separating, one sequence is 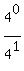 +
+ 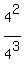 +
+ 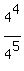 + . . . +
+ . . . + 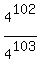 (1)
Another sequence is
(1)
Another sequence is 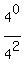 +
+  +
+ 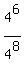 + . . . +
+ . . . + 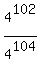 (2)
Sequence (1), after reducing, is the sum of
(2)
Sequence (1), after reducing, is the sum of 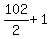 = 52 equal addends, each of which is
= 52 equal addends, each of which is  ,
so this sum is
,
so this sum is 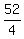 .
Sequence (2), after reducing, is the sum of
.
Sequence (2), after reducing, is the sum of 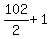 = 52 equal addends, each of which is
= 52 equal addends, each of which is  ,
so this sum is
,
so this sum is  .
Therefore, the total sum is
.
Therefore, the total sum is 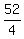 +
+  =
=  +
+  =
= 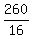 =
= 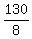 = 16
= 16 = 16
= 16 . ANSWER
. ANSWER
Solved.