Question 1199191: A farmer has 1,310 acres of land on which he grows corn, wheat, and soybeans. It costs $45 per acre to grow corn, $60 to grow wheat, and $50 to grow soybeans. Because of market demand the farmer will grow twice as many acres of wheat as of corn. He has allocated $69,550 for the cost of growing his crops. How many acres of each crop should he plant?
corn acres
wheat acres
soybeans acres
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
A farmer has 1,310 acres of land on which he grows corn, wheat, and soybeans.
It costs $45 per acre to grow corn, $60 to grow wheat, and $50 to grow soybeans.
Because of market demand the farmer will grow twice as many acres of wheat as of corn.
He has allocated $69,550 for the cost of growing his crops.
How many acres of each crop should he plant?
~~~~~~~~~~~~~~~~~~
x = acres for corn;
2x = acres for wheat
1310-x-2x = 1310-3x = acres for soybeans (the rest).
The money equation is
45x + 60*(2x) + 50*(1310-3x) = 69550 dollars.
This equation is in one unknown, and you can easily solve it
45x + 120x + 50*1310 - 150x = 69550
x = 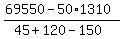 = 270.
ANSWER. 270 acres for corn; 2*270 = 540 acres for wheat, and the rest 1310-270-540 = 500 acres for soybeans.
Solved.
-----------------
The most interesting and educational lesson from this solution is that
the problem can be solved using one equation in one single unknown.
|
|
|
