Question 1199132: Suppose you put $ 525 a month for retirement into an annuity earning 7% compounded monthly. If you need $ 350000 to retire, in how many years will you be able to retire?
Years =
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose you put $ 525 a month for retirement into an annuity earning 7% compounded monthly.
If you need $ 350000 to retire, in how many years will you be able to retire?
~~~~~~~~~~~~~~~~~
The formula for an Ordinary Annuity saving account compounded monthly is
FV = 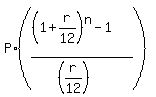 where FV is the future value, P is the annual payment at the end of each month,
r is the interest rate per year expressed as decimal,
n is the number of monthly deposits (of months).
So, we need to find " n " from the equation
where FV is the future value, P is the annual payment at the end of each month,
r is the interest rate per year expressed as decimal,
n is the number of monthly deposits (of months).
So, we need to find " n " from the equation
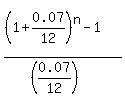 = = 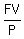 = = 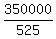 = 666.667,
which is the same as = 666.667,
which is the same as
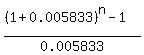 = 666.667.
Rewrite it in this form = 666.667.
Rewrite it in this form
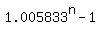 = 0.005833*666.667, = 0.005833*666.667,
 = 1 + 0.005833*666.667 = 4.88867.
Take the logarithm base 10 of both sides
n*log(1.005833) = log(4.88867)
and calculate
n = = 1 + 0.005833*666.667 = 4.88867.
Take the logarithm base 10 of both sides
n*log(1.005833) = log(4.88867)
and calculate
n =  = 272.75 months = 273 months (rounded to the nearest greater integer value) = 22 years and 9 months. ANSWER
CHECK. = 272.75 months = 273 months (rounded to the nearest greater integer value) = 22 years and 9 months. ANSWER
CHECK.  = 350400, which is slightly greater than 350000; = 350400, which is slightly greater than 350000;
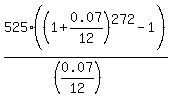 = 347846, which is slightly lesser than 350000.
ANSWER. 273 months is needed, or 22.75 years = 22 years and 9 months.
If to round to closest year, then 23 years is just enough; 22 years is not enough yet. = 347846, which is slightly lesser than 350000.
ANSWER. 273 months is needed, or 22.75 years = 22 years and 9 months.
If to round to closest year, then 23 years is just enough; 22 years is not enough yet.
Solved, checked, explained and completed.
-----------------------
On ordinary annuity saving plan, see my lessons in this site
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
Learn the subject from there.
|
|
|