.
The number 4^1000-1 is divisible by
a) 4
b) 5
c) 7
d) 13
e) 19
~~~~~~~~~~~~~~~~~
I just solved this problem and answered this question several days ago (~ one week ago) under this link
https://www.algebra.com/algebra/homework/equations/Equations.faq.question.1198925.html
https://www.algebra.com/algebra/homework/equations/Equations.faq.question.1198925.html
For your convenience, I copy-paste that my solution here again:
(a) Regarding (a), it is clear that the remainder of division 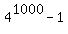 by 4 is -1,
which is the same as 3 mod(4); so,
by 4 is -1,
which is the same as 3 mod(4); so, 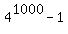 is not divisible by 4.
(b) Regarding (b),
is not divisible by 4.
(b) Regarding (b), 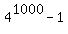 =
= 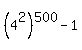 is divisible by
is divisible by 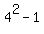 = 15;
so,
= 15;
so, 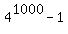 is divisible by 5.
(c, d, e) Regarding (c), (d) and (e), I prepared a table below, which shows the remainders
of division
is divisible by 5.
(c, d, e) Regarding (c), (d) and (e), I prepared a table below, which shows the remainders
of division 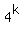 by 7, 13 and 19 respectively.
k
by 7, 13 and 19 respectively.
k 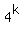 mod(7)
mod(7) 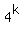 mod(13)
mod(13) 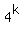 mod(13)
---------------------------------------------------------------
1 4 4 4
2 2 3 16
3 1 12 7
4 4 9 9
5 2 10 17
6 1 1 11
7 4 4 6
8 2 3 5
9 1 12 1
10 4 9 4
3 6 9 <<<---=== the length of the period.
The table shows that for each of these divisors, 7, 13, 19, the sequence of remainders
is periodical, as it should be.
Each period (in each column) starts from the very first term of the sequence.
For mod(7), the remainder 1 is every 3rd term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 3,
mod(13)
---------------------------------------------------------------
1 4 4 4
2 2 3 16
3 1 12 7
4 4 9 9
5 2 10 17
6 1 1 11
7 4 4 6
8 2 3 5
9 1 12 1
10 4 9 4
3 6 9 <<<---=== the length of the period.
The table shows that for each of these divisors, 7, 13, 19, the sequence of remainders
is periodical, as it should be.
Each period (in each column) starts from the very first term of the sequence.
For mod(7), the remainder 1 is every 3rd term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 3, 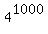 mod(7) is not 1;
hence,
mod(7) is not 1;
hence, 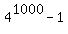 is not divisible by 7.
For mod(13), the remainder 1 is every 6th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 6,
is not divisible by 7.
For mod(13), the remainder 1 is every 6th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 6, 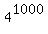 mod(13) is not 1;
hence,
mod(13) is not 1;
hence, 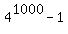 is not divisible by 13.
For mod(19), the remainder 1 is every 9th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 9,
is not divisible by 13.
For mod(19), the remainder 1 is every 9th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 9, 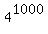 mod(19) is not 1;
hence,
mod(19) is not 1;
hence, 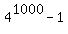 is not divisible by 19.
ANSWER. (a) is not divisible.
(b) is divisible.
(c) is not divisible.
(d) is not divisible.
(e) is not divisible.
is not divisible by 19.
ANSWER. (a) is not divisible.
(b) is divisible.
(c) is not divisible.
(d) is not divisible.
(e) is not divisible.
Solved.