SOLUTION: Determinant matrix hard to type so photo linked below :) Link: https://ibb.co/GP9XwKX

Click here to see ALL problems on Matrices-and-determiminant

Question 1199095: Determinant matrix hard to type so photo linked below :)
Link: https://ibb.co/GP9XwKX

Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website!
.

                Let solve it step by step.

(1) First calculate determinant of the given matrix . Use the basic definition of the determinant in an expanded form. You will get = . (2) It implies, due to well known properties of determinants, that det(A) = = 3. (3) Finally, use another well known formula of linear algebra, which for 3x3 matrix A takes the form det(Adj(A)) = . We just know from (2) that det(A) = 3. Therefore, det(Adj(A)) = = 9. ANSWER. det(Adj(A)) = 9.

Solved, with all necessary explanations.

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

The tutor @ikleyn offers a very efficient (perhaps the most efficient) method.

---------------------------------------------------------

Here's an alternative pathway.
It's much less efficient, but it might be handy to see another route. This longer route is not recommended for homework or exams.
It can be treated as a thought exercise more or less.

One useful properties of adjugate matrices is the following
Det( Adj(A) ) = ( Det(A) )^(n-1)
where n is the number of rows and number of columns of the square matrix A.
In this case we have n = 3.

Because of that formula above, we don't have to calculate the Adj(A) matrix itself.

We're given this inverse matrix

I'll write it in this table format like so

1 a 0
0 1/3 0
0 b 1

To find matrix A itself, aka the inverse of 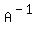, we need to append the 3x3 identity matrix to the right like so

1 a 0 ; 1 0 0
0 1/3 0 ; 0 1 0
0 b 1 ; 0 0 1

The column of semicolons is used to separate out the 3x3 blocks.

The goal is to turn the left-hand 3x3 block into the identity matrix.
The updated right-hand block will be the matrix of
We use row reduction operations to do this transformation.
Notation like 3*R2 --> R2 means we triple each entry of row 2 (aka R2), and store the results in row 2.
A slightly more complicated example is R3-b*R2 --> R3 which means "temporarily multiply each item of R2 by the scalar 'b', then subtract those results from R3. Store the result in R3".
This operation will clear out the pivot below the '1' in R2.

Here's the set of row reduction steps

1 a 0 ; 1 0 0
0 1 0 ; 0 3 0 3*R2 --> R2
0 b 1 ; 0 0 1

1 a 0 ; 1 0 0
0 1 0 ; 0 3 0
0 0 1 ; 0 -3b 1 R3-b*R2 --> R3

1 0 0 ; 1 -3a 0 R1-a*R2 --> R1
0 1 0 ; 0 3 0
0 0 1 ; 0 -3b 1

The left-hand 3x3 block is now the 3x3 identity matrix, which means we conclude this process.
The right-hand 3x3 block forms matrix A.

We find that is the inverse of , and vice versa.

To check this, you should find that and .
I'll leave these two calculations for the student to do.

After determining what matrix A is, we can now compute det(A)
There are a few pathways, but perhaps the simplest (in my opinion) is to follow the steps similar to what is shown here
https://www.algebra.com/algebra/homework/Matrices-and-determiminant/Matrices-and-determiminant.faq.question.1198436.html
I'll leave the steps for the student to do.

Using steps similar to those shown in the link above, if

then

Fortunately a lot of those 0's will make the determinant calculation fairly much easier.

Therefore,
Det(Adj(A)) = ( Det(A) )^(n-1)
Det(Adj(A)) = ( Det(A) )^(3-1)
Det(Adj(A)) = ( Det(A) )^2
Det(Adj(A)) = ( 3 )^2
Det(Adj(A)) = 9

I don't recommend following this process for your homework or exams.
This is simply another way to see why the final answer is 9.
I recommend following the pathway @ikleyn had set out.