Question 1199050: customers are normally distributed: mean age of 32.3 years and a standard deviation of 9.7 years
a) What is the probability that the next customer that enters the store will be in their twenties?
I completed this using normal approximation x=23%
b) What is the probability that 2 of the next 3 customers will be in their twenties?
What I have so far: p=0.23 q=0.77 n=3 but that doesn't fit the normal distribution requirement of >5, so where did I go wrong? Much appreciated.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Let discuss it step by step.
(1) First, I calculate the probability in (a) as
P = normalcfd(20, 30, 32.3, 9.7) = 0.3039.
I consider the age here as the continuous variable (time), not necessary
with integer values: it changes from 20 = 20+0 to 30 = 30-0.
And I got the value of probability 0.3039, different from yours value of 0.23.
(2) This probability that I got (of 0.3039) is not only probability that the next customer will be at his (or her) twenties:
it is the probability that ANY random customer's age is in this interval.
Here they slightly confuse you (intently) with their formulations,
but you should understand, where do they confuse you - it is the rule/(the part) of the game.
(3) Part (b) of the problem relates to Binomial distribution with n= 3 (the number of trials)
and k= 2 (the number of success); p = 0.3039, q = 1-p = 1-0.3039 = 0.6961.
Therefore, P = 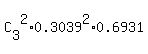 =  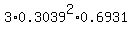= 0.192 (rounded).
Here there is no limitations for the binomial distribution formula: we do not use the normal distribution
as an approximation to the binomial distribution.
We use here the binomial distribution formula as is, for its own correct purposes.
At this point, I complete my explanations.
----------------------------
Do you have questions ? Do you agree ?
Are my logic and numbers consistent with your textbook?
|
|
|
