Question 1198998: A souvenir store wishes to produce two models of souvenirs: Model A and Model B. Every model-A souvenir will result to Php14 profit, and every model-B souvenir will result to Php23 pesos profit. To manufacture a model-A souvenir, it requires 3 minutes on stage 1 and 4 minutes on stage 2. A model-B souvenir requires 5 minutes on stage 1, and 4 minutes on stage 2. There are 270 minutes on stage 1 and 360 minutes on stage 2 for processing order. How many souvenirs of each model should the store make in order to maximize profit?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of model A
y = number of model B
objective function:
profit = 14x + 24y
constraint inequalities:
3x + 5y <= 270
4x + 4y <= 360
x >= 0
y >= 0
using the desmos.com calculator, you would graph the opposite of the inequalities.
the area on the graph that is not shaded is the region of feasibility.
you would evaluate the objective function at each corner point of that feasible region to determine which corner point give you the maximum profit.
the graph is shown below.

the point (0,54) gives you a profit of 54 * 23 = 1242.
the point (90,0) gives you a profit of 90 * 14 = 1260.
your maximum profit is at the point (90,0) where you build 90 model A souvenirs and 0 model B souvenirs.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A souvenir store wishes to produce two models of souvenirs: Model A and Model B.
Every model-A souvenir will result to Php14 profit, and
every model-B souvenir will result to Php23 pesos profit.
To manufacture a model-A souvenir, it requires 3 minutes on stage 1 and 4 minutes on stage 2.
A model-B souvenir requires 5 minutes on stage 1, and 4 minutes on stage 2.
There are 270 minutes on stage 1 and 360 minutes on stage 2 for processing order.
How many souvenirs of each model should the store make in order to maximize profit?
~~~~~~~~~~~~~~~~~~~~
The plots in the post by @Theo are INCORRECT.
Therefore, I came to bring a correct solution.
Let X be the number of model A souvenirs;
Y be the number of model B souvenirs.
objective function:
P(X,Y) = 14X + 23Y
constraint inequalities:
3X + 5Y <= 270 (minutes on stage 1)
4X + 4Y <= 360 (minutes on stage 2)
x >= 0, y >= 0
The feasible domain is shown in the plot below
 Plots y =
Plots y = 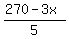 (red) and y = (red) and y =  (green)
From the plot, you see that the feasibility domain is a triangle in QI under the red line.
It has the vertices
(X1,Y1) = (0,0) (the origin of the coordinate system);
(X2,Y2) = (0,54) (red line Y-intercept);
(X3,Y3) = (90,0) (red line X-intercept).
The values of the objective function at these points are
R(X1,Y1) = 14*0 + 23*0 = 0;
R(X2,Y2) = 14*0 + 23*54 = 1242;
R(X3,Y3) = 14*90 + 23*0 = 1260.
The objective function is maximal at the point (X3,Y3) = (90,0).
Hence, the optimal solution is X = 90 souvenirs of model A and Y = 0 souvenirs of model B.
If they follow this optimal solution, their maximum profit will be Php 1260. (green)
From the plot, you see that the feasibility domain is a triangle in QI under the red line.
It has the vertices
(X1,Y1) = (0,0) (the origin of the coordinate system);
(X2,Y2) = (0,54) (red line Y-intercept);
(X3,Y3) = (90,0) (red line X-intercept).
The values of the objective function at these points are
R(X1,Y1) = 14*0 + 23*0 = 0;
R(X2,Y2) = 14*0 + 23*54 = 1242;
R(X3,Y3) = 14*90 + 23*0 = 1260.
The objective function is maximal at the point (X3,Y3) = (90,0).
Hence, the optimal solution is X = 90 souvenirs of model A and Y = 0 souvenirs of model B.
If they follow this optimal solution, their maximum profit will be Php 1260.
Solved.
|
|
|