SOLUTION: 5. Convert the following equation into vertex form by completing the square. f(x) = 2x^2+12x-4

The vertex form of a parabola is:

 where (h,k) is the vertex.



Factor 2 out of the first two terms only:



We must add and subtract the proper number inside the parentheses to
cause 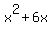 to become a perfect square.  To do that we take
1/2 of the coefficient of x, which is 6.  1/2 of 6 is 3.  Then we
square 3 and get 9.  So 9 is the number we must add, then subtract,
i.e., +9-9 inside the parentheses:



Next we factor only the first three terms inside the parentheses:



And, as you see it factors as the square of a binomial:



Next we distribute the 2 into the parentheses leaving the (x+3)2 intact.





Comparing to 

 where (h,k) is the vertex.

The vertex is (h,k) = (-3,-22)

Edwin