Question 1198830: A ball is thrown off the top of a building. At time t (in seconds) its height (in feet) follows the path described by the function f(t)=-3t^2 + 24t +60. What is the ball maximum height?
The correct answer is one of the following. Which one is it?
A) 8 feet
B) 24 feet
C) 60 feet
D) 108 feet
Found 3 solutions by MathLover1, ikleyn, math_tutor2020:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52802)  (Show Source):
You can put this solution on YOUR website! .
A ball is thrown off the top of a building. At time t (in seconds) its height (in feet) follows
the path described by the function f(t)=-3t^2 + 24t +60. What is the ball maximum height?
~~~~~~~~~~~~~~~~
From the Physics point of view, the equation in the post
for the height of a ball at free fall conditions is written incorrectly.
If you have the formula for a height given to you as a function of time in the form
h(t) = -at^2 + bt + c, (1)
where "a", "b" and "c" are real numbers, a > 0, then in this formula
(a) the initial height is equal to the coefficient "c" value;
(b) the initial velocity is the coefficient "b" in the formula;
(c) the coefficient "a" value is half of the gravity acceleration.
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h =  , substitute h = into equation (1)
and solve equation
h(t) = -at^2 + bt + c = . (2)
(f) To find the time when the height is maximal, use the formula
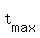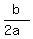 =  . (3)
(g) To find the maximal height, substitute the time value t= 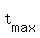of the formula (3) into the formula (1).
That's all you need to know.
After my explanations, you can solve the problem on YOUR OWN now,
but for it, you should have your governing equation written correctly.
---------------
To see numerous examples of solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Let's complete the square.
f(t) = -3t^2 + 24t + 60
f(t) = (-3t^2 + 24t) + 60
f(t) = -3(t^2 - 8t) + 60
f(t) = -3(t^2 - 8t + 16 - 16) + 60
f(t) = -3((t^2 - 8t + 16) - 16) + 60
f(t) = -3((t-4)^2 - 16) + 60
f(t) = -3(t-4)^2 -3(-16) + 60
f(t) = -3(t-4)^2 + 48 + 60
f(t) = -3(t-4)^2 + 108
The equation is now in vertex form.
Think of
f(t) = -3(t-4)^2 + 108
as
y = -3(x-4)^2 + 108
Then compare that to the general vertex form template.
y = a(x-h)^2+k
Vertex = (h,k) = (4, 108)
This represents the highest point due to a = -3 being negative (the parabola opens downward).
The highest the ball reaches is 108 feet, and this max height occurs when t = 4 seconds.
Answer: D) 108 feet
|
|
|
