|
Question 1198739: The product of two numbers is 51. Find the numbers if the
sum of three times one number and the other is as large as
possible. Find them if the same sum is as small as possible.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 51 is equal to 51 * 1 or 17 * 3.
there are no other integers whose product is 51.
3 * 51 + 1 = 154
3 * 1 + 51 = 52
3 * 17 + 3 = 54
3 * 3 + 17 = 26
the numbers that give the largest sum would be 51 and 1.
the numbers that give the smallest sum would be 3 and 17.
that what i think.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The product of two numbers is 51. Find the numbers if the
sum of three times one number and the other is as large as
possible. Find them if the same sum is as small as possible.
~~~~~~~~~~~~~~~~~
Let one number be x; then the other number is 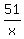 .
The problem asks two questions:
(a) find real value of x providing the maximum x + .
The problem asks two questions:
(a) find real value of x providing the maximum x + 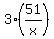 = x + = x + 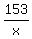 (if exists);
(b) find real value of x providing the minimum x + (if exists);
(b) find real value of x providing the minimum x + 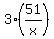 = x + = x + 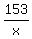 (if exists).
Answer to question (a) is THIS:
+-------------------------------------+
| such number x does not exist. |
+-------------------------------------+
Indeed, we can take positive value of x as large as we want (any real positive number).
Then the addend (if exists).
Answer to question (a) is THIS:
+-------------------------------------+
| such number x does not exist. |
+-------------------------------------+
Indeed, we can take positive value of x as large as we want (any real positive number).
Then the addend 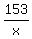 will be small, but still positive, making the sum x + will be small, but still positive, making the sum x + 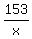 even greater.
Answer to question (b) is SIMILAR:
+-------------------------------------+
| such number x does not exist. |
+-------------------------------------+
Indeed, we can take negative value of x as small as we want (any real negative number).
Then the addend even greater.
Answer to question (b) is SIMILAR:
+-------------------------------------+
| such number x does not exist. |
+-------------------------------------+
Indeed, we can take negative value of x as small as we want (any real negative number).
Then the addend 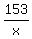 will be negative number, making the sum x + will be negative number, making the sum x + 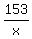 even smaller.
The plot of the function f(x) = x + even smaller.
The plot of the function f(x) = x + 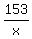 is shown below.
It makes it graphically obvious my answers, saying that this given function has
NEITHER global maximum, NOR global minimum. is shown below.
It makes it graphically obvious my answers, saying that this given function has
NEITHER global maximum, NOR global minimum.
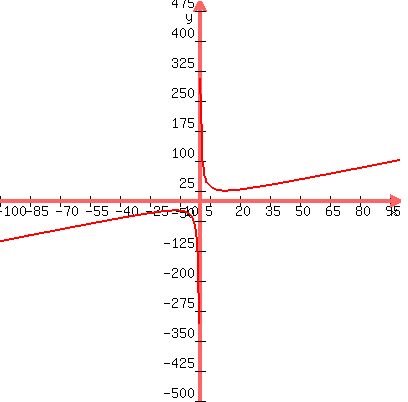 Plot f(x) =
Plot f(x) =  + + 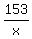
Solved, answered and explained.
As worded, the problem has no solution.
Function f(x) has local minimum and maximum, but not global minimum and maximum.
Therefore, in order for the problem does really have solution/solutions, it should be
worded/posed in different way.
How you will pose it in correct way, depends on you - I do not want to guess the ideas
inside your head.
////////////////
The other tutor considers only positive integer numbers in his response,
although the problem does not impose these restrictions;
so, his answer and his solution/consideration is not relevant to the problem.
|
|
|
| |