SOLUTION: Consider the equation, 4x^2-18x=3. What number must be added to both sides of the equation in order to complete the square?

Algebra ->  Equations -> SOLUTION: Consider the equation, 4x^2-18x=3. What number must be added to both sides of the equation in order to complete the square?      Log On


   

Question 1198731: Consider the equation, 4x^2-18x=3. What number must be added to both sides of the equation in order to complete the square?
Found 4 solutions by ikleyn, Alan3354, MathLover1, MathTherapy:
Answer by ikleyn(52783) About Me  (Show Source):
You can put this solution on YOUR website!
.
Consider the equation, 4x^2-18x=3. What number must be added
to both sides of the equation in order to complete the square?
~~~~~~~~~~~~~~~~ 

The leading term with  x^2  is  4x^2 = (2x)^2.


Therefore, you should add the term c^2, where you determine the value of "c" 
from this equality

    2*(2c) = -18,  which gives  c = 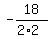-18%2F%282%2A2%29 = -41%2F2  = -4.5.


The term to add to both sides is (-4.5)^2 = 20.25.    ANSWER

Solved.

---------------

On solving quadratic equations using completing the square method,  look into the lesson
    - HOW TO solve quadratic equation by completing the square - Learning by examples
in this site.


//////////////


What Alan recommends in his post, is incorrect. 

The correct addend is 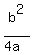 b%5E2%2F%284a%29,  referring to the general equation form

    ax^2 + bx = -c.


\\\\\\\\\\\\\\\\


Do not even read the post by @MathLover1, if you want to save your mind,

since her recommendation is totally wrong: it relates to the modified leading part equation,

while the problem asks about the addend to UNMODIFIED leading part equation.



Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Consider the equation, 4x^2-18x=3. What number must be added to both sides of the equation in order to complete the square?
--------------
Add %28b%2F2a%29%5E2
===========================
NUM Lock wasn't on, the 2 got lost.

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

The rule we use for completing the square is that if we add %28b%2F2%29%5E2 to both sides of the equation in order to complete the square.
But if a general quadratic equation have a coefficient of a in front of x%5E2:
ax%5E2+%2B+bx+%2B+c+=+0
we just divide the whole equation by "a" first, then carry on:
x%5E2+%2B+%28b%2Fa%29x+%2B+c%2Fa+=+0


4x%5E2-18x=3............divide the whole equation by 4
x%5E2-%2818%2F4%29x=3%2F4
x%5E2-%289%2F2%29x=3%2F4............. the coefficient of the x term is b=9%2F2, so %28b%2F2%29%5E2=+%28%289%2F2%29%2F2%29%5E2=%289%2F4%29%5E2, add to both sides
x%5E2-%289%2F2%29x%2B%289%2F4%29%5E2=3%2F4%2B%289%2F4%29%5E2
%28x%5E2-9%2F4%29%5E2=3%2F4%2B81%2F16
%28x%5E2-9%2F4%29%5E2=93%2F16

so, you need to add %289%2F4%29%5E2 to both sides


Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Consider the equation, 4x^2-18x=3. What number must be added to both sides of the equation in order to complete the square?
Correct number to be added: 

Accept NO OTHER answer!

As usual, anything MATHLOVER - Don't know how this name came about - says, it's advisable to do the opposite, ignore, or DUMP!!!