SOLUTION: Paul bought a number of shares of stock for a total of $3000.Three months later the stock had increased in value by $5 per share and he sold all but 50 shares and regained his orig

Let n be the number of shares Paul sold.

Then the original number of shares he bought was (n+50).


The buying price per share was 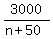  dollars.

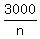The selling price per share was  dollars.


The difference of these prices was 5 dollars, according to the problem,
which gives this "price" equation


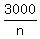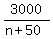     -  = 5  dollars.     (1)


To solve this equation, multiply both sides by n*(n+50), then simplify step by step


    3000*(n+50) - 3000*n = 5n*(n+50)

    3000n + 150000 - 3000n = 5n^2 + 250n

    5n^2 + 250n - 150000 = 0

     n^2 +  50n -  30000 = 0

     (n+200)*(n-150) = 0


The equation has two roots, -200 and 150.  
Of these two roots, we discard the negative one and accept the positive value n= 150.


CHECK.  To check, substitute n= 150 into equation (1). You will get

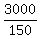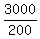         -  = 20 - 15 = 5,  which is precisely correct.


ANSWER.  Paul sold 150 shares.