Question 1198404: In hw many ways can three items be selected from a group of six items. Use letters A B C D E and F to identity the items and list each of the different combination of three items
Found 2 solutions by Edwin McCravy, math_tutor2020:
Answer by Edwin McCravy(20059)   (Show Source):
You can put this solution on YOUR website!
This is the number of combinations of 6 things taken 3 at a time.
{A,B,C} {A,B,D} {A,B,E} {A,B,F} {A,C,D}
{A,C,E} {A,C,F} {A,D,E} {A,D,F} {A,E,F}
{B,C,D} {B,C,E} {B,C,F} {B,D,E} {B,D,F}
{B,E,F} {C,D,E} {C,D,F} {C,E,F} {D,E,F}
20 ways. The formula is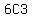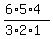     
To form the numerator, the first factor is the number we have to select from,
then the next factor is 1 less, and the next factor is 1 less than that, etc. if
necessary. We stop when the number of factors is equal to the number we are
choosing.
To form the denominator, the first factor is the number we are choosing, and
the next factor is 1 less, and the next factor is 1 less, etc. if necessary. We
stop when we get to 1. There should be the same number of factors in the
denominator as in the denominator.
Form the fraction, then simplify to an integer.
Edwin
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
There are 6 choices for the first slot, then 6-1 = 5 choices for the second slot, and finally 5-1 = 4 choices for the third slot.
If order mattered, then we'd have 6*5*4 = 30*4 = 120 different permutations, and this would be the final answer.
But order doesn't matter.
The group {A,B,C} is the same as something like {B,A,C}.
The order doesn't matter when considering the group overall.
There are 3*2*1 = 6 ways to rearrange any given group of 3 items.
This tells us that the previous figure of 120 is too large by a factor of 6.
Divide by 6 to correct for this over-counting: 120/6 = 20
Therefore, we have 20 different groups of three letters chosen from a pool of six.
Alternatively you can use the nCr combination formula to get this answer.
Use n = 6 and r = 3.
Another alternative is to use Pascal's Triangle.
Look at the row that starts with 1,6,... and you're looking for the item in the fourth slot.
This is because the 'r' value starts counting at r = 0 rather than r = 1.
Answer: 20
|
|
|
