Question 1198366: How many different 4-letter permutations can be formed from the letters in the word REPRESENT?
I know that if I want deffrent letter it would be permutation
like 6P4 = 360
but how about the repeated letters like the E 3 times and r 2 times?
Found 3 solutions by ikleyn, ewatrrr, Edwin McCravy:
Answer by ikleyn(52805)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many different 4-letter permutations can be formed from the letters in the word REPRESENT?
I know that if I want deffrent letter it would be permutation
like 6P4 = 360
but how about the repeated letters like the E 3 times and r 2 times?
~~~~~~~~~~~~~~~~~~~~
Since they want you use different letters with no repetition,
you should first determine the number of different letters in the word REPRESENT.
It is easy to do: the number of different letters is R + E + P + S + N + T = 6.
Now you apply the method which you know, and you get this answer:
the number of different 4-letter permutations is 6*5*4*3 = 360
(four consecutive integer factors in descending order, starting from the number of 6).
Solved, with complete explanations.
--------------
Another interpretation is possible considering/allowing repeating letters.
@ewatrr tried to implement it, but her calculations are erroneous.
See my calculations for this case below.
There are 6 different letters; of them, letter "E" has multiplicity 3
and letter "R" has multiplicity 2.
We have 360 permutations without repetition, as I counted above.
Next, with 3 "E" and one single letter from remaining 5 letters {R,P,S,N,T} we have 5*4 = 20 additional permutations.
Next, with 2 "E" and 2 "R", we have  = =  = 6 additional distinguishable permutations.
Next, with 2 "E" and 2 other single letters from the remaining 6-1 = 5 other unique letters {R,P,S,N,T},
we have = 6 additional distinguishable permutations.
Next, with 2 "E" and 2 other single letters from the remaining 6-1 = 5 other unique letters {R,P,S,N,T},
we have 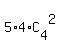 = 20*6 = 120 additional distinguishable permutations.
Next, with 2 "R" and 2 other single letters from the remaining 6-1 = 5 other unique letters {E,P,S,N,T},
we have = 20*6 = 120 additional distinguishable permutations.
Next, with 2 "R" and 2 other single letters from the remaining 6-1 = 5 other unique letters {E,P,S,N,T},
we have 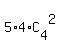 = 20*6 = 120 additional distinguishable permutations.
In all, there are 360 + 20 + 6 + 120 + 120 = 626 permutations of this kind. ANSWER = 20*6 = 120 additional distinguishable permutations.
In all, there are 360 + 20 + 6 + 120 + 120 = 626 permutations of this kind. ANSWER
So, you have solutions for both possible interpretations.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many different 4-letter permutations can be formed from the letters in the word REPRESENT?
Singles(e, n , r , s, t) with duplicate letters (eee,rr)
My Imput:
No Duplicates: 6P4 = 360 0r (6C4)x4! = 360
1 from single and eee: (5C1)(1C1)x4!/3! = 20
2 from single and 1 pair of duplicate letter: (5C2)((2C1)4!/2! = 240
2 pair of duplicate letters: (2C2)4!/2!2! = 6
How many different 4-letter permutations can be formed from the letters in the word REPRESENT?
How many would be the Sum= 360 + 20 +240+ 6 = 626
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is the correct solution, which is 626.
Break them down into 4 types: AAAB-type, AABB-type, AABC-type, and ABCD-type.
Each distinguishable 4-letter arrangement that can be made from the letters in
the word REPRESENT can be made by replacing the letters A,B,C,D in some
distinguishable arrangement of one of these AAAB, AABB, AABC, or ABCD, by
letters from the set {R,E,P,S,N,T}
Case 1. AAAB. There are 4!/3!=4 distinguishable arrangements of AAAB.
For each of those 4 arrangements of AAAB, we can replace the A 1 way (as E),
and we can then replace the B by any of the other 5 letters. So there are 4*1*5=20
distinguishable arrangements of the AAAB-type.
Case 2. AABB. There are 4!/(2!2!)=6 distinguishable arrangements of AABB.
For each of those 6 distinguishable arrangements of AABB, there is only one way
to choose a combination of letters to replace the combination {A,B} by and that
one combination is the combination {R,E}. So there are 6*1=6 distinguishable
arrangements of the AABB-type.
Case 3. AABC. There are 4!/2!=12 distinguishable arrangements of AABC.
For each of those 12 arrangements of AABC, we can replace the A 2 ways (R or E),
and we can then replace the B by any of the other 5 unselected letters. Then we
can replace the C by any of the remaining 4 unselected letters. So there are
12*5*4=240 distinguishable arrangements of the AABC-type.
Case 4. ABCD. There are 4!=24 arrangements of ABCD, all distinguishable. For
each of these 24, we can replace A,B,C,D with a permutation of these 6 things
{R,E,P,S,N,T} taken 4 at a time. That's 6P4 = 6*5*4*3 = 360 distinguishable
arrangements of the ABCD-type.
That gives a total of 20+6+240+360 = 626.
Below are all 626 distinguishable 4-letter arrangements from REPRESENT,
computer-generated. 48 full rows of 13 each. That's 48*13=624 plus the
49th row only has 2.
REPR, REPE, REPS, REPN, REPT, RERP, RERE, RERS, RERN, RERT, REEP, REER, REES,
REEE, REEN, REET, RESP, RESR, RESE, RESN, REST, RENP, RENR, RENE, RENS, RENT,
RETP, RETR, RETE, RETS, RETN, RPER, RPEE, RPES, RPEN, RPET, RPRE, RPRS, RPRN,
RPRT, RPSE, RPSR, RPSN, RPST, RPNE, RPNR, RPNS, RPNT, RPTE, RPTR, RPTS, RPTN,
RREP, RREE, RRES, RREN, RRET, RRPE, RRPS, RRPN, RRPT, RRSE, RRSP, RRSN, RRST,
RRNE, RRNP, RRNS, RRNT, RRTE, RRTP, RRTS, RRTN, RSEP, RSER, RSEE, RSEN, RSET,
RSPE, RSPR, RSPN, RSPT, RSRE, RSRP, RSRN, RSRT, RSNE, RSNP, RSNR, RSNT, RSTE,
RSTP, RSTR, RSTN, RNEP, RNER, RNEE, RNES, RNET, RNPE, RNPR, RNPS, RNPT, RNRE,
RNRP, RNRS, RNRT, RNSE, RNSP, RNSR, RNST, RNTE, RNTP, RNTR, RNTS, RTEP, RTER,
RTEE, RTES, RTEN, RTPE, RTPR, RTPS, RTPN, RTRE, RTRP, RTRS, RTRN, RTSE, RTSP,
RTSR, RTSN, RTNE, RTNP, RTNR, RTNS, ERPR, ERPE, ERPS, ERPN, ERPT, ERRP, ERRE,
ERRS, ERRN, ERRT, EREP, ERER, ERES, EREE, EREN, ERET, ERSP, ERSR, ERSE, ERSN,
ERST, ERNP, ERNR, ERNE, ERNS, ERNT, ERTP, ERTR, ERTE, ERTS, ERTN, EPRR, EPRE,
EPRS, EPRN, EPRT, EPER, EPES, EPEE, EPEN, EPET, EPSR, EPSE, EPSN, EPST, EPNR,
EPNE, EPNS, EPNT, EPTR, EPTE, EPTS, EPTN, EERP, EERR, EERS, EERE, EERN, EERT,
EEPR, EEPS, EEPE, EEPN, EEPT, EESR, EESP, EESE, EESN, EEST, EEER, EEEP, EEES,
EEEN, EEET, EENR, EENP, EENS, EENE, EENT, EETR, EETP, EETS, EETE, EETN, ESRP,
ESRR, ESRE, ESRN, ESRT, ESPR, ESPE, ESPN, ESPT, ESER, ESEP, ESEE, ESEN, ESET,
ESNR, ESNP, ESNE, ESNT, ESTR, ESTP, ESTE, ESTN, ENRP, ENRR, ENRE, ENRS, ENRT,
ENPR, ENPE, ENPS, ENPT, ENER, ENEP, ENES, ENEE, ENET, ENSR, ENSP, ENSE, ENST,
ENTR, ENTP, ENTE, ENTS, ETRP, ETRR, ETRE, ETRS, ETRN, ETPR, ETPE, ETPS, ETPN,
ETER, ETEP, ETES, ETEE, ETEN, ETSR, ETSP, ETSE, ETSN, ETNR, ETNP, ETNE, ETNS,
PRER, PREE, PRES, PREN, PRET, PRRE, PRRS, PRRN, PRRT, PRSE, PRSR, PRSN, PRST,
PRNE, PRNR, PRNS, PRNT, PRTE, PRTR, PRTS, PRTN, PERR, PERE, PERS, PERN, PERT,
PEER, PEES, PEEE, PEEN, PEET, PESR, PESE, PESN, PEST, PENR, PENE, PENS, PENT,
PETR, PETE, PETS, PETN, PSRE, PSRR, PSRN, PSRT, PSER, PSEE, PSEN, PSET, PSNR,
PSNE, PSNT, PSTR, PSTE, PSTN, PNRE, PNRR, PNRS, PNRT, PNER, PNEE, PNES, PNET,
PNSR, PNSE, PNST, PNTR, PNTE, PNTS, PTRE, PTRR, PTRS, PTRN, PTER, PTEE, PTES,
PTEN, PTSR, PTSE, PTSN, PTNR, PTNE, PTNS, SREP, SRER, SREE, SREN, SRET, SRPE,
SRPR, SRPN, SRPT, SRRE, SRRP, SRRN, SRRT, SRNE, SRNP, SRNR, SRNT, SRTE, SRTP,
SRTR, SRTN, SERP, SERR, SERE, SERN, SERT, SEPR, SEPE, SEPN, SEPT, SEER, SEEP,
SEEE, SEEN, SEET, SENR, SENP, SENE, SENT, SETR, SETP, SETE, SETN, SPRE, SPRR,
SPRN, SPRT, SPER, SPEE, SPEN, SPET, SPNR, SPNE, SPNT, SPTR, SPTE, SPTN, SNRE,
SNRP, SNRR, SNRT, SNER, SNEP, SNEE, SNET, SNPR, SNPE, SNPT, SNTR, SNTE, SNTP,
STRE, STRP, STRR, STRN, STER, STEP, STEE, STEN, STPR, STPE, STPN, STNR, STNE,
STNP, NREP, NRER, NREE, NRES, NRET, NRPE, NRPR, NRPS, NRPT, NRRE, NRRP, NRRS,
NRRT, NRSE, NRSP, NRSR, NRST, NRTE, NRTP, NRTR, NRTS, NERP, NERR, NERE, NERS,
NERT, NEPR, NEPE, NEPS, NEPT, NEER, NEEP, NEES, NEEE, NEET, NESR, NESP, NESE,
NEST, NETR, NETP, NETE, NETS, NPRE, NPRR, NPRS, NPRT, NPER, NPEE, NPES, NPET,
NPSR, NPSE, NPST, NPTR, NPTE, NPTS, NSRE, NSRP, NSRR, NSRT, NSER, NSEP, NSEE,
NSET, NSPR, NSPE, NSPT, NSTR, NSTE, NSTP, NTRE, NTRP, NTRR, NTRS, NTER, NTEP,
NTEE, NTES, NTPR, NTPE, NTPS, NTSR, NTSE, NTSP, TREP, TRER, TREE, TRES, TREN,
TRPE, TRPR, TRPS, TRPN, TRRE, TRRP, TRRS, TRRN, TRSE, TRSP, TRSR, TRSN, TRNE,
TRNP, TRNR, TRNS, TERP, TERR, TERE, TERS, TERN, TEPR, TEPE, TEPS, TEPN, TEER,
TEEP, TEES, TEEE, TEEN, TESR, TESP, TESE, TESN, TENR, TENP, TENE, TENS, TPRE,
TPRR, TPRS, TPRN, TPER, TPEE, TPES, TPEN, TPSR, TPSE, TPSN, TPNR, TPNE, TPNS,
TSRE, TSRP, TSRR, TSRN, TSER, TSEP, TSEE, TSEN, TSPR, TSPE, TSPN, TSNR, TSNE,
TSNP, TNRE, TNRP, TNRR, TNRS, TNER, TNEP, TNEE, TNES, TNPR, TNPE, TNPS, TNSR,
TNSE, TNSP
Edwin
|
|
|