SOLUTION: You are given an unfair coin with probability of obtaining a head equal to 1/3, 000, 000, 000. You toss this coin 6,000,000,000 times. Let A be the event that you get “tails fo

Algebra ->  Probability-and-statistics -> SOLUTION: You are given an unfair coin with probability of obtaining a head equal to 1/3, 000, 000, 000. You toss this coin 6,000,000,000 times. Let A be the event that you get “tails fo      Log On


   

Question 1198328: You are given an unfair coin with probability of obtaining a head equal to
1/3, 000, 000, 000. You toss this coin 6,000,000,000 times. Let A be the
event that you get “tails for all the tosses”. Let B be the event that you get
“heads for all the tosses”.
i) Approximate P (A).
ii) Approximate P (A ∪ B)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Let N+be the number of heads among the n tosses. Then, N ∼ B(n,+p).
given:
probability of obtaining a head equal to:1%2F3000000000=1%2F%283+%2A10%5E9%29
You toss this coin 6000000000=+6%2A10%5E9 times

Here, we have small p+=+1%2F%283+%2A10%5E9%29 and large n+=+6%2A10%5E9. So, we can apply Poisson approximation.
In other words, B(n,+p) is well-approximated by P%28alpha%29 where alpha+=+np+=+2.

(a)
P%28A%29 = P [N+=+0] = e%5E-2%282%5E0%2F0%21%29=1%2Fe%5E2≈ 0.1353
(b)
P(A ∪ B)= P [N+=+0]+P [N+=+n] = e%5E-2%282%5E0%2F0%21%29%2Be%5E-2%28%282%5E6%2A10%5E9%29%2F%286%2A10%5E9%29%21%29
The second term is extremely+small compared to the first one.
Hence, P(A ∪ B) is approximately the same as P%28A%29.

Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.
You are given an unfair coin with probability of obtaining a head equal to 1/3, 000,000,000.
You toss this coin 6,000,000,000 times. Let A be the event that you get “tails for all the tosses”.
Let B be the event that you get “heads for all the tosses”.
i) Approximate P (A).
ii) Approximate P (A ∪ B)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

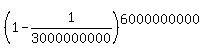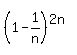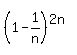For (i),  P(A) = %281-1%2F3000000000%29%5E6000000000 = %281-1%2Fn%29%5E%282n%29,

          where n = 3,000,000,000.


          From Calculus, it is well known fact that  

               lim %281-1%2Fn%29%5E%282n%29 = e%5E%28-2%29  as n --> oo.


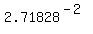          So, P(A) = e%5E%28-2%29 = 2.71828%5E%28-2%29 = 0.1353  (approximately).    ANSWER



For (ii), P(B) is extremely small and events A and B are mutially exclusive;

          therefore, P(A U B) = P(A): P(B) contributes practically nothing.

Solved.