.
The altitude of a pyramid is 12 cm. A parallel to the base cut the pyramid into two solids of equal volumes.
The distance of the cutting plane from the vertex is expressed as d = α^3√β cm where α and β are integers.
Find the smallest sum of α and β.
~~~~~~~~~~~~~~~
Your formulation in the post is INCORRECT.
I was so kind that re-wrote the problem in a right form.
The correct version is as follows:
The altitude of a pyramid is 12 cm. A parallel to the base cut the pyramid into two solids of equal volumes.
The distance of the cutting plane from the vertex is expressed as d =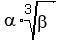 
cm, where α and β are integers.
Find the smallest sum of α and β.
See my solution below for this corrected version.
Let x be the distance from the vertex to the cutting plane.
The cut part and the whole pyramid are similar solids, so the ratio
of their volumes (which is 1:2) is the cube of the ratio of their
respective linear elements.
It gives us this proportion
= 
,
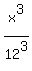or
x^3 =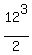 
= 
= 
= 
.
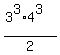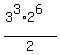Hence, x =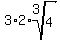 
= 
.
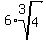Thus 
= 6, 
= 4, and the sum + = 6 + 4 = 10. ANSWER
Solved.
