Question 1198149: Write the complex number in polar form with argument 𝜃 between 0 and 2𝜋.
negative square root of 3 minus i
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The number  is of the form is of the form  with these particular values with these particular values


which is the same as saying  and and  when describing this rectangular point in (x,y) form. when describing this rectangular point in (x,y) form.
A number in polar form is 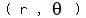
The 'r' talks about the distance from the origin to the location of (x,y).
In this case, r is the distance from (0,0) to 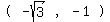
Use this formula

which is derived from the pythagorean theorem (note that  ) )
So,





The distance from (0,0) to 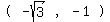 is exactly 2 units. is exactly 2 units.
-----------------------------------------------
Now to compute the angle theta.
 arctan is the same as inverse tangent arctan is the same as inverse tangent



 where theta is in radian mode where theta is in radian mode
This is equivalent to 30 degrees and we're in quadrant Q1.
But wait, the point 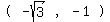 is clearly in quadrant Q3 since both x and y are negative. We'll need to add on is clearly in quadrant Q3 since both x and y are negative. We'll need to add on  radians (aka 180 degrees) to apply a half rotation to arrive at the proper quadrant. radians (aka 180 degrees) to apply a half rotation to arrive at the proper quadrant.

So the actual value of theta is 
-----------------------------------------------
To summarize the last two sections, we found that
 and and 
This gives the polar form of 
Some textbooks and/or teachers will require you to write the answer in the format 
If that's the case, then your final answer would be  which condenses down to which condenses down to 
The "cis" stands for "cosine i sine" in that order.
This shortened notation is very useful for formulas involving multiplying complex numbers, as it makes the process much easier.
|
|
|