SOLUTION: Business Weekly conducted a survey of recent graduates from the top MBA programs. On the basis of the survey, assume that 75% of the recent graduates annual salary exceeds $75000.

This problem is a binomial distribution with the number of trials n= 86,
the probability of the individual success p= 75% = 0.75 and the number of 
succesful trials k > 0.85*86 = 73.1.


Since n*p = 86*p.75 = 73.1 is greater than 5 and since n*(1-p) = 86*0.15 = 12.9 is greater than 5,
the basis is provided to apply the normal approximation to the binomial approximation.


So, we take the normal distribution with the mean m= p*n = 0.85*86 = 73.1 and the standard
deviation SD = 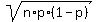 =  = 3.3113  (rounded).


It is the normal distribution which we use as an approximation.


Now the probability under the problem's question is the are under the this specified normal curve 
to the RIGHT of the mark of 73.5 (the continuity correction).


You can use your calculator's standard function normalcdf(73.5,9999,73.1,3.3113)
or the Internet's free of charge online calculator https://onlinestatbook.com/2/calculators/normal_dist.html
to get the  ANSWER  P = 0.4519.


You may also want to calculate this probability directly as the binomial probability.

In this case, use an online free of charge calculator https://stattrek.com/online-calculator/binomial

    P(n= 86, k> 73, p= 0.85) = 0.46596.


Both values are quite close, giving you the needed confidence.