SOLUTION: What remainder is left when the number {{{(567288133)^6}}} is divided by 8?

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: What remainder is left when the number {{{(567288133)^6}}} is divided by 8?      Log On


   

Question 1197923: What remainder is left when the number 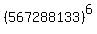%28567288133%29%5E6 is divided by 8?
Found 3 solutions by MathLover1, ikleyn, math_tutor2020:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
567288133%5E6%2F8=4166124127573669059244469709874775759816632193744721%2B1%2F8
so,
567288133%5E6=4166124127573669059244469709874775759816632193744721%2A8%2B1

reminder is 1

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.

It is easy to check directly that  567288133  gives the remainder  5  when divided by  8.

By the way, for it, only three last digits of a number are important.


    We write  567288133 == 5 mod 8.


It means that 567288133%5E6  gives the remainder  5%5E6 when divided by 8.


    Next,  5%5E6 = 15625.


It is also easy to check directly that the remainder  {15625 mod 8}  is the same as  {1 mod 8}.

    (and again, for it, only three last digits of the number 15625 do matter).


ANSWER.  When the number %28567288133%29%5E6 is divided by 8, the remainder is 1.

Solved.


///////////////////


May the god save you from solving this problem in the way as @MathLover1 does it . . .



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Recall the divisibility by 8 rule says that we only need to look at the last 3 digits of the number to see if the number is a multiple of 8 or not.

This means numbers like
800
1800
11800
111800
are all multiples of 8 since 800, in the last three digits, is a multiple of 8.

Then note how 8*16 = 128
So numbers like
128
4128
54128
754128
are all multiples of 8 because 128 is a multiple of 8.

Furthermore, adding 5 more to each number causes us to get a remainder of 5 when dividing by 8.

128+5 = 133
133/8 = something remainder 5

4128+5 = 4133
4133/8 = something remainder 5

54128+5 = 54133
54133/8 = something remainder 5

and so on.

In short, the last three digits of 133 indicate we'll get a remainder of 5 when dividing it over 8.

So even if the number 567288133 is really massive, we only need to care about the 133 at the end.
133/8 = something remainder 5
567288133/8 = something remainder 5
We don't need to worry about the quotient, so I just labeled it as "something".

This leads 567288133^6 to reduce to 5^6 mod 8.

Let's look at powers of 5 mod 8.
Meaning that I'll divide numbers of the form 5^k over 8 to determine the remainder
5^1 = 5 (mod 8)

5^2 = 5*5 (mod 8)
5^2 = 25 (mod 8)
5^2 = 1 (mod 8) since 25 is 1 more than 24 = 3*8

5^3 = 5*5^2 (mod 8)
5^3 = 5*25 (mod 8)
5^3 = 5*1 (mod 8) .... replace 25 with 1 mod 8
5^3 = 5 (mod 8)
This tells us that dividing 5^3 over 8 gets us a remainder of 5.

5^4 = 5*5^3 (mod 8)
5^4 = 5*5 (mod 8) .... replace 5^3 with 5 mod 8
5^4 = 25 (mod 8)
5^4 = 1 (mod 8)

As you can see, we get this pattern of remainders: 5, 1, 5, 1, ...
It cycles forever like this.

If the exponent k is odd, then 5^k = 5 (mod 8)
If the exponent k is even, then 5^k = 1 (mod 8)

Therefore, 5^6 = 1 (mod 8) because of the even number exponent
i.e. (5^6)/8 = something remainder 1

Check:
5^6 = 15625
15625/8 = 1953.125 = 1953 remainder 1

Answer: 1