Question 1197922: How many integer solutions (a,b,c) make the equation  true?
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website! the equation true if:
 = ± ,  = ±  ,  = ± 
= ± , = ±  ,  = ± 
 = ± , = ± , = ±
= ± , = ± , = ±
= ± , = ± , = ±
:
:
:
= ± , = ± , = ±
:
 , = ±  , 
total number of integer solutions:
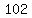
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
If a,b,c are nonnegative integers where  then the only integer solutions to  are the following
(a,b,c) = (0,0,17)
(a,b,c) = (0,8,15)
(a,b,c) = (1,12,12)
(a,b,c) = (8,9,12)
These four solutions are found through trial-and-error. Note that the second class (0,8,15) is from the pythagorean triple 8,15,17 which gives the equation 8^2+15^2 = 17^2 from the pythagorean theorem.
Let's remove the requirement that .
So we can permute the elements, meaning something like (0,0,17) leads to (0,17,0) and (17,0,0). There are 3 such permutations.
Let's now remove the requirement that the numbers a,b,c must be nonnegative.
That yields twice as many solutions to give us 3*2 = 6 different solutions just based on the class (a,b,c) = (0,0,17). This is because the 17 could represent +17 or -17.
The class (0,8,15) has 3! = 3*2*1 = 6 permutations
The 8 could be +8 or -8; the 15 could be +15 or -15
So we multiply by 2*2 = 4 to get 4*6 = 24 different solutions from the class (a,b,c) = (0,8,15)
The class (1,12,12) has 3! = 6 permutations if we could tell the '12's apart; however we cannot. So we divide by 2 to fix this erroneous double-counting to get 6/2 = 3 permutations instead.
Each item could be positive or negative, so we multiply by 2^3 = 2*2*2 = 8 to get 8*3 = 24 different solutions of the class (a,b,c) = (1,12,12)
Lastly, the class (a,b,c) = (8,9,12) has 3! = 6 permutations. Each shows up 2 times to get us 2*2*2*6 = 8*6 = 48 different solutions here.
| class | count | | 0,0,17 | 6 | | 0,8,15 | 24 | | 1,12,12 | 24 | | 8,9,12 | 48 |
From here we add up the frequencies to get
6+24+24+48 = 102
which is the number of integer solutions to
Answer: 102
|
|
|
