Question 1197831: Find all the rational root of the equation 9x ^ 4 - 12x ^ 3 + 13x ^ 2 - 12x + 4 = 0
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @MathLover1 often posts responses to questions like this where she shows a factorization obtained by grouping the terms in a particular way. There is nothing in her responses that shows the student (or anyone else) HOW to do the grouping to make the factoring work. I have posted many responses to those responses of hers asking her to explain how to choose the right way to do the grouping, but she has never responded. So as far as I know, she finds the roots using a graphing calculator and works backwards from those roots to find the correct way to do the factoring.
As her response to this question stands, it teaches the student nothing....
Given this problem, I would first use Descartes' rule of signs to find that the number of positive real roots is either 4 or 2 or 0, and that the number of negative real roots is 0.
Then I would use the rational roots theorem to show that the possible positive real roots are 1, 2, 4, 1/3, 2/3, 4/3, 1/9, 2/9, and 4/9.
Quick substitution shows that 1 is not a root; and I would not be inclined to test the other roots without first looking for another approach to the problem.
So now I would look for a way to group the terms to find a factorization.
What catches my eye is the -12x^3 and -12x terms, so I would do my grouping like this:
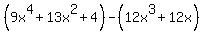
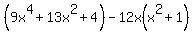
Then, seeing that factor of (x^2+1) in the second term, I would take another look at the first term to find
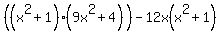
which gives
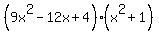
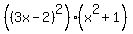
So the roots are when 3x-2=0 and when x^2+1=0.
The first equation gives us the real root 2/3; the second gives us the imaginary (complex) root i and -i.
ANSWER: the single rational root of the equation is x = 2/3
|
|
|