|
Question 1197815: Hi, can you solve this? with a solution and the formula to use, thankyou.
The vertices of a triangle are at ( 4, 5 ), ( -7, -6 ) and ( 10, -3 ). Show that the line joining the midpoints of any two sides is equal to one-half of the third side.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52817)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let
A = ( 4, 5 )
B = ( -7, -6 )
C = ( 10, -3 )
represent the vertices of the triangle.
Furthermore we'll have
P = midpoint of AB
Q = midpoint of BC
R = midpoint of AC
Drawing:

To compute the midpoint, we add up the x coordinates and divide in half.
Let's do this for points A(4,5) and B(-7,-6)
Add: 4 + (-7) = -3
Cut in half: -3/2 = -1.5
This is the x coordinate of point P
Do the same for the y coordinates
Add: 5 + (-6) = -1
Cut in half: -1/2 = -0.5
Point P is located at (-1.5, -0.5)
Here's what you should get for points P through R
P = (-1.5, -0.5)
Q = (1.5, -4.5)
R = (7, 1)
I'll skip the steps showing how to locate Q and R, but you'd follow similar steps when I found P.
-----------------------------------------------------
Definition: A midsegment is a segment connecting two midpoints of a triangle.
We have these three midsegments
PQ
PR
QR
Let's use the distance formula to find the distance from B(-7,-6) to C(10,-3)
(x1,y1) = (-7,-6) and (x2,y2) = (10,-3)



Segment BC is exactly  units long. units long.
Now let's find the distance from P(-1.5, -0.5) to R(7, 1)
(x1,y1) = (-1.5,-0.5) and (x2,y2) = (7,1)



Midsegment PR is exactly 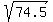 units long. units long.
Compute the ratio of BC and PR.




We can then rearrange that like so



Showing us that midsegment PR is exactly half as long compared to BC.
-----------------------------------------------------
Repeat these sets of steps to show these two other facts


I'll let the student do these.
|
|
|
| |