Question 1197786: If the tangent of an angle is positive and the secant of the angle is negative, in which quadrant does the angle terminate?
A. I
B. II
C. III
D. IV
E. Information given is not sufficient to determine.
Found 4 solutions by MathLover1, Alan3354, math_tutor2020, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In Quadrant I, 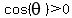 , , 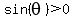 and and 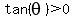 (All positive). (All positive).
In Quadrant II, 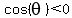 , , 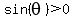 and and 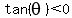 (Sine positive). (Sine positive).
In Quadrant III, 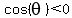 , , 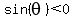 and and 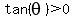 (Tangent positive). (Tangent positive).
In Quadrant IV, 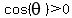 , , 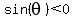 and and 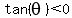 (Cosine positive). (Cosine positive).
so,
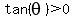 in quadrant I, III in quadrant I, III
Secant is reciprocal of cosine which is negative in the II and III quadrant, so
 in quadrant II,III in quadrant II,III
answer is: C. III
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
sin = sine
cos = cosine
sec = secant
tan = tangent
tan = sin/cos
sec = 1/cos
Since tangent is positive, this means sin/cos is positive.
This further means one of the the following (pick one)
- sin > 0 and cos > 0 (quadrant I)
- sin < 0 and cos < 0 (quadrant III)
We also know secant is negative, which makes 1/cos negative and cosine is also negative.
Recall that
x = cos(theta)
If cosine is negative then we're to the left of the y axis in either quadrant II or quadrant III.
But we know we're not in quadrant II because of the previous info mentioned. We must be in quadrant III.
I recommend reviewing a unit circle.
Answer: C. III
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the tangent of an angle is positive and the secant of the angle is negative, in which quadrant does the angle terminate?
A. I
B. II
C. III
D. IV
E. Information given is not sufficient to determine.
Acronym: ASTC, which stands for: All: ALL Trigonometric Ratios are POSITIVE in Quadrant I
Students: SINE and ALL of its affiliated Trigonometric Ratios are POSITIVE in Quadrant II
Take: TANGENT and ALL of its affiliated Trigonometric Ratios are POSITIVE in Quadrant III
Calculus: COSINE and ALL of its affiliated Trigonometric Ratios are POSITIVE in Quadrant IV
Given that TANGENT is positive, the angle can terminate in either Quadrant I or III. However, since the SECANT (affiliated
with COSINE, as it's 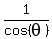 ) of the angle is NEGATIVE, the angle DEFINITELY terminates in the 3rd Quadrant (CHOICE C.). ) of the angle is NEGATIVE, the angle DEFINITELY terminates in the 3rd Quadrant (CHOICE C.).
|
|
|