SOLUTION: 750 eggs are randomly sampled from a population where 14% of all eggs are fertilized. Use the normal approximation to the binomial to find the following probabilities rounded to 3

Click here to see ALL problems on Probability-and-statistics

Question 1197774: 750 eggs are randomly sampled from a population where 14% of all eggs are fertilized. Use the normal approximation to the binomial to find the following probabilities rounded to 3 decimal places.

a. Find the probability that exactly 106 of the eggs are fertilized.
b. Find the probability that at least 106 of the eggs are fertilized.
c. Find the probability that fewer than 106 of the eggs are fertilized.
d. Find the probability that between 104 and 106, inclusive, of the eggs are fertilized.
Answer by ewatrrr(24785) (Show Source):
You can put this solution on YOUR website!

Hi Binomial distribution: p - .14, n = 750 Using the normal approximation and the NOted continuity correction factor. (the continuity correction factor used as a Binomial Distribution is not continuous) µ = .14*750 = 105, and σ = 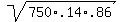= 9.5026 Using TI or similarly an inexpensive calculator like an Casio fx-115 ES plus a. P(x = 106) = binompdf(750,.14,106) = .042 0r normpdf( 106,105,9.5026) = .042 with continuity correction factor, normcdf(105.5,106.5, 9.5026, 105)=.042 b. P x ≥ 106) = normcdf(105.5,9999, 9.5026, 105) = .479 c. P(x<106) = P(x <105.5) = normcdf(-9999,105.5, 9.5026, 105)= .521 d. P(104 ≤ x ≤ 106) = normcdf(103.5,106.5, 9.5026, 105) =.1254 Wish You the Best in your Studies.