|
Question 1197771: The midpoints of the sides of a triangle are at ( 0, -3 ), ( -1/2, 7/2 ), and ( -7/2, 1⁄2 )
Find the coordinates of the vertices.
Found 3 solutions by MathLover1, math_tutor2020, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1/2 = 0.5
7/2 = 3.5
We have a triangle with unknown vertices.
The midpoints of this triangle are
A = (0, -3)
B = (-0.5, 3.5)
C = (-3.5, 0.5)
The motion from B to C is "down 3, left 3"
We'll follow that motion pattern when starting at point A.
Start at A(0,-3) and move down 3, left 3 to arrive at (-3,-6) which is one of the vertices of the triangle. Label this as point D.
D = (-3,-6)
Notice that ABCD is a parallelogram.

The motion from A to B is "left 0.5, up 6.5"
Follow this pattern when starting at point C and you should arrive at (-4,7) which I'll call point E.
E = (-4,7)
This is another vertex of the triangle we're after.
The motion from C to A is "right 3.5, down 3.5"
Follow this pattern when starting at point B and you should arrive at (3,0) which I'll call point F.
F = (3,0)
Therefore, triangle DEF has the midpoints A,B,C mentioned.
D = (-3,-6)
E = (-4,7)
F = (3,0)

Use the midpoint formula to confirm that- point A is the midpoint of segment DF
- point B is the midpoint of segment EF
- point C is the midpoint of segment DE
I'll let the student perform these confirmations.
-----------------------------------------------------------
Answers:
(-3,-6)
(-4, 7)
(3, 0)
The order of the points doesn't matter.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the given points be A(0,-3), B(-0.5,3.5), and C(-3.5,0.5).
Draw the triangle with those points as vertices.

The lines joining the midpoints of a triangle are parallel to and half the length of the sides of the triangle. So we can find the vertices of the triangle we want by copying any of the sides of triangle ABC in both directions from the opposite vertex.
For example, segment BC can be described informally as "left 3, down 3". We can find two of the vertices of the triangle we are looking for by going "left 3, down 3" from A and by going "right 3, up 3" from vertex A:
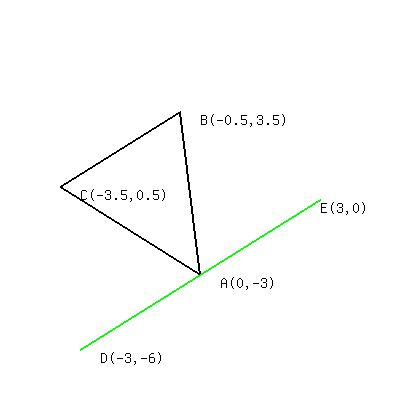
Then, to find the third vertex of the triangle we are looking for, we can either copy segment AC starting from B, or copy segment AB starting from C. The next drawing shows segment AC ("left 3.5, up 3.5") copied starting from B:

We have found the three vertices of the triangle we are looking for; we can show the triangle by drawing the missing segments.

|
|
|
| |