Question 1197767: Which of the following is not a fourth root of -8 + 8i*square root of 3
A. square root of 3 - i
B. square root of 3 + i
C. -1 + i*square root of 3
D. -square root of 3 -i
E. 1 - i*square root of 3
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Which of the following is not a fourth root of -8 + 8i*square root of 3
A. square root of 3 - i
B. square root of 3 + i
C. -1 + i*square root of 3
D. -square root of 3 -i
E. 1 - i*square root of 3
~~~~~~~~~~~~~~~~~
The number 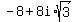 has the modulus of 16 and the argument of 120°.
Hence, the fourth roots of this number have the modulus 2 and arguments 30°, 120°, 210° and 300°.
Number A = has the modulus of 16 and the argument of 120°.
Hence, the fourth roots of this number have the modulus 2 and arguments 30°, 120°, 210° and 300°.
Number A = 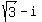 has the modulus 2 and the argument arg(A) = 330°.
So, number A is NOT a fourth degree root of the given number.
Number B = has the modulus 2 and the argument arg(A) = 330°.
So, number A is NOT a fourth degree root of the given number.
Number B =  has the modulus 2 and the argument arg(B) = 30°.
So, number B is one of the fourth degree roots of the given number.
Number C = has the modulus 2 and the argument arg(B) = 30°.
So, number B is one of the fourth degree roots of the given number.
Number C = 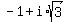 has the modulus 2 and the argument arg(C) = 120°.
So, number C is one of the fourth degree root of the given number.
Number D = has the modulus 2 and the argument arg(C) = 120°.
So, number C is one of the fourth degree root of the given number.
Number D = 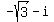 has the modulus 2 and the argument arg(D) = 210°.
So, number D is one of the fourth degree roots of the given number.
Number E = has the modulus 2 and the argument arg(D) = 210°.
So, number D is one of the fourth degree roots of the given number.
Number E = 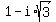 has the modulus 2 and the argument arg(E) = 300°.
So, number E is one of the fourth degree roots of the given number.
ANSWER. There is only one number from the list which is NOT a fourth degree root of has the modulus 2 and the argument arg(E) = 300°.
So, number E is one of the fourth degree roots of the given number.
ANSWER. There is only one number from the list which is NOT a fourth degree root of 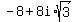 : it is number (A). : it is number (A).
Solved, with explanations.
-------------
In my solution, I freely use properties of the roots and degrees of complex numbers (like de Moivre theorem
and other equivalent statements) even without referring.
It is because this knowledge is a PRE-Requisite for solution of this problem - so, it is assumed
that you just know everything of it.
On complex numbers, see my lessons in this site
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
- Solved problems on taking roots of complex numbers
- Solved problems on arithmetic operations on complex numbers
- Solved problem on taking square root of complex number
- Miscellaneous problems on complex numbers
- Advanced problem on complex numbers
- Solved problems on de'Moivre formula
- Calculating the sum 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)
- A curious example of an equation in complex numbers which HAS NO a solution
- Solving one non-standard equation in complex numbers
- Determine locus of points using complex numbers
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|