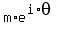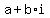 can be written
can be written  ∠
∠ 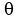 ("m angle theta"),
("m angle theta"),
where:
m = 
and
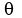 =
= 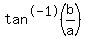
For 3+i: m = 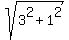 =
= 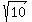
 =
= 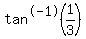 or approx. 18.435 degrees.
or approx. 18.435 degrees.
Now, to find the square root, just take the square root of m and divide the angle 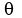 by two:
by two:
sqrt(3+i) = 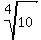 ∠
∠ 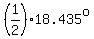
or approx. = 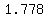 ∠
∠ 
If you must express this as 'a + bi' form (rectangular form):
a = m * cos( ) = 1.778*cos(9.218) = 1.755
) = 1.778*cos(9.218) = 1.755
b = m * sin( ) = 1.778*sin(9.218) = 0.285
) = 1.778*sin(9.218) = 0.285
so 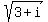 ≈
≈ 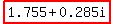
---
EDIT: the notation I used really comes from Electrical Engineering, but keep in mind it is just shorthand for a+bi =