|
Question 1197748: When A,B and C work together, they can finish
installing the garden in 3 days. The job could be
completed of A worked 4 days alone and
C worked 10 days alone or if B worked 5 days alone and C worked 3 days alone. How many days would it take each worker alone to complete the garden?
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When A,B and C work together, they can finish installing the garden in 3 days.
The job could be completed of A worked 4 days alone and C worked 10 days alone
or if B worked 5 days alone and C worked 3 days alone.
How many days would it take each worker alone to complete the garden?
~~~~~~~~~~~~~~~~~~~
Let "a" be the A's rate of work, in job per day;
"b" be the B's rate of work, in job per day;
"c" be the C's rate of work, in job per day.
From the condition, we have this system of 3 equations in 3 unknowns
a + b + c =  , (1)
4a + 10c = 1, (2)
5b + 3c = 1. (3)
To solve, express a = , (1)
4a + 10c = 1, (2)
5b + 3c = 1. (3)
To solve, express a = 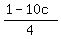 from (2), and express b = from (2), and express b =  from (3).
Substitute these expressions into equation (1). You will exclude "b" and "c" from (1)
and will get single equation for unknown "c" from (3).
Substitute these expressions into equation (1). You will exclude "b" and "c" from (1)
and will get single equation for unknown "c"
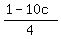 + +  + c = + c =  . (4)
Multiply both sides by 60
15(1-10c) + 12*(1-3c) + 60c = 20
15 - 150c + 12 - 36c + 60c = 20
27 - 126c = 20
27 - 20 = 126c
7 = 126c
c = . (4)
Multiply both sides by 60
15(1-10c) + 12*(1-3c) + 60c = 20
15 - 150c + 12 - 36c + 60c = 20
27 - 126c = 20
27 - 20 = 126c
7 = 126c
c = 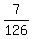 = =  .
It means that C will complete the job in 18 days working alone.
Now a = .
It means that C will complete the job in 18 days working alone.
Now a = 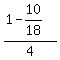 = =  = =  = =  ;
b = ;
b = 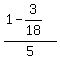 = =  = = 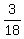 = =  .
ANSWER. A can complete the job in 9 days working alone;
B can complete the job in 6 days working alone;
C can complete the job in 18 days working alone. .
ANSWER. A can complete the job in 9 days working alone;
B can complete the job in 6 days working alone;
C can complete the job in 18 days working alone.
Solved.
|
|
|
| |