SOLUTION: Find the smallest positive integer n such that the base ten representation of 2 at the power of n has exactly 500 digits.

We want to find smallest possible integer n in such a way that

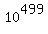     >=     (notice that  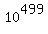 is the smallest integer number requiring 500 digits in base 10).


So, we have this simple inequality. To solve it, take logarithm base 10 of both sides.  
You will get this inequality

    n*log(2) >= 499

    n >= 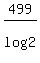 = now use your calculator = 1657.642  (rounded).


To get that integer n, you must round the decimal 1657.642  to the nearest greater integer, which is, by the case, 1658.


ANSWER.  1658 is the smallest positive integer n such that the base ten representation 
         of 2 at the power of n has exactly 500 digits.