SOLUTION: The vertices of a triangle are at ( 4, 5 ), ( -7, -6 ) and ( 10, -3 ). Show that the line joining the midpoints of any two sides is equal to one-half of the third side.

Algebra ->  Length-and-distance -> SOLUTION: The vertices of a triangle are at ( 4, 5 ), ( -7, -6 ) and ( 10, -3 ). Show that the line joining the midpoints of any two sides is equal to one-half of the third side.      Log On


   

Question 1197714: The vertices of a triangle are at ( 4, 5 ), ( -7, -6 ) and ( 10, -3 ). Show that the line
joining the midpoints of any two sides is equal to one-half of the third side.
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Let
A = (4,5)
B = (-7,-6)
C = (10,-3)
be the three given points we have.

Furthermore we'll have
P = midpoint of AB
Q = midpoint of AC
R = midpoint of BC

This is what the diagram looks like, which was generated using GeoGebra.


To determine the locations of P,Q,R, we apply the midpoint formula.
This is where we add the x coordinates together and divide in half, and do the same for the y coordinates.


-----------------------------
An example:

The x coordinates of A and B are 4 and -7 respectively.
They add to 4+(-7) = -3 which cuts in half to -3/2 = -1.5
This is the x coordinate of the midpoint.

The y coordinates of A and B are 5 and -6 respectively.
They add to 5+(-6) = -1 and cut in half to -1/2 = -0.5
This is the y coordinate of the midpoint.

Point P is then located at (-1.5, -0.5) whiich is the midpoint of segment AB.

Follow similar steps for points Q and R.
-----------------------------

You should arrive at these midpoint locations
P = (-1.5, -0.5)
Q = (7,1)
R = (1.5, -4.5)
as shown in the diagram above.

Let's pick on two of the midpoints, say P and Q.
The claim is that midsegment PQ is half as long as side BC.

Let's use the distance formula on B(-7,-6) and C = (10,-3)
(x1,y1) = (-7,-6) and (x2,y2) = (10,-3)

d+=+sqrt%28+%28x1-x2%29%5E2+%2B+%28y1-y2%29%5E2+%29

d+=+sqrt%28+%28-7-10%29%5E2+%2B+%28-6-%28-3%29%29%5E2+%29

d+=+sqrt%28+298+%29
Segment BC is exactly sqrt%28298%29 units long.

Use the distance formula to find that segment PQ is exactly 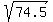sqrt%2874.5%29 units long.

Then notice how
%28BC%29%2F%28PQ%29+=+%28sqrt%28298%29%29%2F%28sqrt%2874.5%29%29

%28BC%29%2F%28PQ%29+=+sqrt%28298%2F74.5%29

%28BC%29%2F%28PQ%29+=+sqrt%284%29

%28BC%29%2F%28PQ%29+=+2

BC+=+2%2APQ
Showing that side BC is twice as long as midsegment PQ
I.e. PQ is half as long as BC.

This idea will be applied to show the other midsegments (PR and RQ) are half as long as the side not involved with any midpoints attached to them.
I'll let the student handle these cases. Let me know if you have any questions.

For more information, search out "triangle midsegment proof".