Question 1197695: A consumer group claims that the average annual consumption of high fructose corn syrup by a person in the U.S. is 48.8 pounds. You believe it is higher. You take a simple random sample of 34 people in the U.S. and find an average of 53.8 pounds with a standard deviation of 6 pounds. Test at 10% significance
We can work this problem because:
Select an answer
H
0
:
Select an answer
Select an answer
H
A
:
Select an answer
Select an answer
Test Statistic:
P-value:
Did something significant happen?
Select an answer
Select the Decision Rule:
Select an answer
There
Select an answer
enough evidence to conclude
Found 2 solutions by ewatrrr, math_tutor2020:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Ho: µ = 48.8
Ha: µ > 48.8
n = 34, x̄ = 53.8 s = 6
As population sd is not known, used a t-test vs a z- test (either is fine n >30)
0.10 significance level, Critical value = 1.3077 (df 33)
 = 4.859
4.859 > 1.3077 Reject Ho
P(z ≤ 4.859, df 33) = .00001 < .05 Reject Ho
If Using a Standard z-Distribution:
4.859 > 1.282 Reject Ho
P(z ≤ 4.859) = .0000006 < .05 Reject Ho
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
n = 34 = sample size
xbar = 53.8 = sample mean
s = 6 = sample standard deviation
mu = population mean
sigma = population standard deviation
Sigma is unknown, which is a common occurrence in stats.
Despite sigma being unknown, we can use the Z distribution because n > 30.
The T distribution is approximately fairly close to the standard Z distribution for these large values of n.
If sigma were unknown and n < 30, then we'd have to use the T distribution.
Hypothesis:
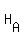 : mu = 48.8
 : mu > 48.8
The claim is in the alternative hypothesis.
This gives us a right tailed test.
Computing the test statistic:
z = (xbar - mu)/(s/sqrt(n))
z = (53.8 - 48.8)/(6/sqrt(34))
z = 4.85912657903776
z = 4.86
Use a Z calculator to find that
P(Z > 4.86) = 0.000000587
which is the approximate p-value.
I don't know how the tutor @ewatrrr got P(z ≤ 4.859) = .000014 as that is not correct.
This p-value 0.000000587 is very small.
Depending how you round this, the p-value is effectively 0.
Whenever the p-value is smaller than alpha, we reject the null.
We conclude that mu > 48.8 appears to be the case.
-------------------------------------------------
If you wanted to go the critical value route, then at 10% significance, the critical value is roughly z = 1.28 since P(Z > 1.28) = 0.10 approximately
The test statistic (z = 4.86) is to the right of the critical value (z = 1.28), which places the test statistic in the rejection region.
This is another way to see why we reject the null in favor of the alternative hypothesis.
|
|
|
