SOLUTION: A triangle, PQR, has P(8, 0), Q(0, −8) and point R is on the line y = x − 2. Find the area of the triangle PQR.

Algebra ->  Linear-equations -> SOLUTION: A triangle, PQR, has P(8, 0), Q(0, −8) and point R is on the line y = x − 2. Find the area of the triangle PQR.      Log On


   

Question 1197616: A triangle, PQR, has P(8, 0), Q(0, −8) and point R is on the line y = x − 2. Find the area of the
triangle PQR.
Answer by math_tutor2020(3816) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: 24 square units

===========================================================================

Explanation:

At first glance, this seems like a problem that might suggest an answer of "infinitely many positive areas are possible" due to the fact point R slides anywhere along the line y = x-2. If not infinitely many, then perhaps it suggests at least more than one possible answer.

However, there's only one possible answer since the line y = x-2 runs parallel to line PQ.
You can graph the items mentioned to confirm this claim, or you can use algebraic tools mentioned below.

Apply the slope formula to points P and Q to find that...
P = (x1,y1) = (8,0)
Q = (x2,y2) = (0,-8)
m+=+%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29

m+=+%28-8+-+0%29%2F%280+-+8%29

m+=+%28-8%29%2F%28-8%29

m+=+1
The slope of line PQ is 1, which matches with the slope of y = x-2, aka y = 1x-2.

Either line PQ is parallel to line y = x-2, or we're talking about the same line.

But there's no way they could be the same line because the y intercept of line PQ is Q(0,-8).
In contrast, the y intercept of y = x-2 is (0,-2)
Therefore, these two lines are parallel and never intersect.

Side note: parallel lines have equal slopes, but different y intercepts.

What we can do is rotate the page so that line PQ is horizontal.
The height of the triangle runs perpendicular from line PQ to line y = x-2.
This height does not change as the distance between the parallel lines remains constant. Think of railroad tracks being the same width apart all throughout.

--------------------------------------------------

So far we've established that there's only one possible height for this triangle when we treat PQ as the base.
This leads to exactly one area value (even if R is sliding around wherever you want).

Let's use the distance formula to find the length of side PQ
(x1,y1) = (8,0) and (x2,y2) = (0,-8)
d+=+sqrt%28+%28x1-x2%29%5E2+%2B+%28y1-y2%29%5E2+%29

d+=+sqrt%28+%288-0%29%5E2+%2B+%280-%28-8%29%29%5E2+%29

d+=+sqrt%28+%288-0%29%5E2+%2B+%280%2B8%29%5E2+%29

d+=+sqrt%28+%288%29%5E2+%2B+%288%29%5E2+%29

d+=+sqrt%28+64+%2B+64+%29

d+=+sqrt%28+128+%29

d+=+sqrt%2864%2A2%29

d+=+sqrt%2864%29%2Asqrt%282%29

d+=+8%2Asqrt%282%29

Side PQ is exactly 8%2Asqrt%282%29 units long, which I'll treat as the base of triangle PQR. If needed, rotate the page so PQ is horizontal.

Next, we'll need to find the height perpendicular to side PQ.

Let's find the equation of the line perpendicular to y = x-2 that goes through P(8,0)
I'll apply point-slope form.
y - y1 = m(x - x1)
y - 0 = -1(x - 8)
y = -x + 8

This perpendicular line (y = -x+8) intersects line y = x-2 at some point, why not call it R.
Use whichever method you prefer to find R(5,3)
This will make triangle PQR a right triangle with the 90 degree angle at point P.

Then use the distance formula to find the length of side PR
I'll skip steps, but you should get 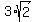3%2Asqrt%282%29

We can now compute the area of triangle PQR.
area+=+0.5%2Abase%2Aheight

area+=+0.5%2APQ%2APR

area+=+0.5%2A8%2Asqrt%282%29%2A3%2Asqrt%282%29

area+=+12%2Asqrt%282%2A2%29

area+=+12%2Asqrt%284%29

area+=+12%2A2

area+=+24
The area of triangle PQR is 24 square units

This applies for any triangle where R can slide around freely along y = x-2, and not just a right triangle.

You can use software tools like GeoGebra to confirm the answer. I use it all the time and recommend it to any geometry or algebra students.