Question 1197611: If 0 < x < pi/4 is such that cscx - secx = (13^1/2)/6, then cotx - tanx equals
Found 2 solutions by ewatrrr, math_tutor2020:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The goal is to find the value of 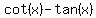 based on based on  and the restriction and the restriction 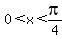
Note: 
Let's simplify 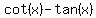 a bit like shown below a bit like shown below
You'll need a list of trig identities such as this here
https://tutorial.math.lamar.edu/pdf/Trig_Cheat_Sheet.pdf
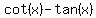
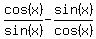

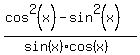
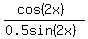
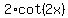
In short, 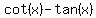 is the same as is the same as 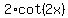
 is an identity. is an identity.
Keep this in mind for later.
----------------------------------------------------------
Now let's solve for x in 






 Squaring both sides Squaring both sides



 Let w = sin(2x) Let w = sin(2x)
Let's solve for w.




Use the quadratic formula (I'll skip showing the steps) to find that the two roots for w are
w = -12 or w = 12/13
We're told that
0 < x < pi/4
Multiply each side by 2
2*0 < 2x < 2*pi/4
0 < 2x < pi/2
Then apply sine to each
sin(0) < sin(2x) < sin(pi/2)
0 < sin(2x) < 1
This shows that the output of sin(2x) must be between 0 and 1, which rules out w = -12 aka sin(2x) = -12
Also, the range of sin(x) is  . So even if we didn't have to worry about 0 < x < pi/4, it's still impossible to have sin(2x) = -12 (not unless we want to involve complex numbers, but we'll stay in the real number set). . So even if we didn't have to worry about 0 < x < pi/4, it's still impossible to have sin(2x) = -12 (not unless we want to involve complex numbers, but we'll stay in the real number set).
We'll ignore w = -12 and go for w = 12/13 only.
Therefore, sin(2x) = 12/13
Isolating x gets us x = 0.5*arcsin(12/13)
There are infinitely many solutions to sin(2x) = 12/13, but again we focus on the interval 0 < x < pi/4, which means we only have one solution.
Note: arcsine is the same as inverse sine aka )
----------------------------------------------------------
Recall the ultimate goal is to find 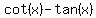 which we found was equivalent to which we found was equivalent to 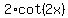
Plug in x = 0.5*arcsin(12/13) and simplify
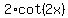
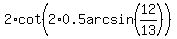
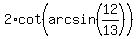
The question now is: how can we evaluate cot(arcsin(12/13))?
Let theta = arcsin(12/13) which rearranges to sin(theta) = 12/13
Since sine = opposite/hypotenuse, this gives us a right triangle with opposite leg 12 and hypotenuse 13.
Use the pythagorean theorem to find the adjacent leg is 5 units.
We have a 5-12-13 right triangle (this is one of the infinitely many pythagorean triples).

Tangent is the ratio of opposite/adjacent
the reciprocal is cotangent which is adjacent/opposite
So cot(theta) = adjacent/opposite = 5/12
which means,

Therefore,

when 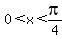 and and 
----------------------------------------------------------
----------------------------------------------------------
Answer: 5/6
|
|
|