Question 1197471: A car covered a certain distance at a speed of 24 mph. While returning, the car covered the same distance at a speed of 16 mph. What was the average speed of the car for the entire journey?
Found 5 solutions by josgarithmetic, ikleyn, math_tutor2020, greenestamps, ewatrrr:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! ---------------------------------------------------
A car covered a certain distance at a speed of
24 mph. While returning, the car covered the same distance at a speed of 16 mph. What was the average speed of the car for the entire journey?
-----------------------------------------------
---------------------------------------------------
A car covered a certain distance d at a speed of
H mph. While returning, the car covered the same distance at a speed of L mph. What was the average speed of the car for the entire journey?
-----------------------------------------------
SPEED TIME DISTANCE
GOING H d/H d
RETURNING L d/L d
TOTALS d/H+d/L 2d
Average speed for whole round trip,
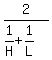 -----simplify this. Substitute your given values and compute. -----simplify this. Substitute your given values and compute.
19.2 mph
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use the formula for average speed for any round trip
 = = 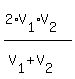 = = 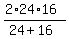 = 19.2 mph. ANSWER = 19.2 mph. ANSWER
Solved.
About this formula, and to see other similar solved problems, look into the lessons
- Calculating an average speed: a train going from A to B and back
- One more problem on calculating an average speed
at this site.
///////////////
Regarding the opinions of other tutors, expressed in their posts, I can only say that, when I attended my middle school,
knowing of this formula and knowing of its roots, as well as an ability to deduce it and to use it consciously was a  . .
Twenty years after school, you may forget it; but while at the school, you MUST know it.
Also, think a minute about this: how will you solve this problem, if the given rates are not integer numbers, but are the decimal, instead ?
Will you find their common multiple then ?
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Edit: The distance doesn't need to be an integer, so the use of LCM is optional. The method I used works for any positive real number distance. I selected integers to make the numbers more digestible.
The use of the formulas mentioned by the other tutors is a great approach, if you understand what is going on, and understand how the formulas work.
I don't recommend blindly memorizing them unless you are under a time crunch (say for an upcoming exam).
I'll take a different approach.
The GCF of 24 and 16 is 8
The LCM of 24 and 16 is 24*16/GCF = 24*16/8 = 48
Let's say the distance from point A to B is 48 miles.
There's nothing special about this value, so feel free to pick something else.
I selected it so that the next two division operations result in whole numbers.
Going from A to B, the car travels 48 miles at a speed of 24 mph
distance = rate*time
time = distance/rate
time = 48/24
time = 2 hours.
Then when going from B to A, it travels a speed of 16 mph
time = distance/rate = 48/16 = 3 hours
The total distance is 48+48 = 96 miles for the entire round trip
The total time taken is 2+3 = 5 hours. We only account for traveling time and not moments when the car is stopped (eg: when the car is getting gas)
Then as the final step
distance = rate*time
rate = distance/time
rate = 96/5
rate = 19.2 mph as the final answer
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I definitely agree with tutor @Math_tutor2020 that it is better to solve the problem by a method that you understand, rather than by blindly plugging numbers into a magic formula.
Here is an informal solution method that is similar to his, yet very different.
The ratio of the two speeds is 24:16 = 3:2, and the distances there and back are the same. That means the ratio of the times at the two speeds is 2:3.
So 2/5 of the total time is spent at 24mph and 3/5 of the total time is spent at 16mph. The average speed in mph is then

ANSWER: 96/5 = 19.2 miles per hour
Answer by ewatrrr(24785)   (Show Source): (Show Source):
|
|
|